![]()
![]()
![]()
![]()
![]()
![]()
![]()
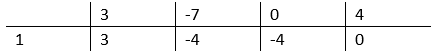
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
ODP: Wymiary prostopadłościanu o najmniejszym polu całkowitym wynoszą
![]() .
.

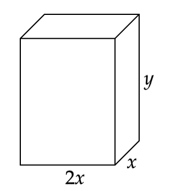
Wykonaj rysunek pomocniczy:
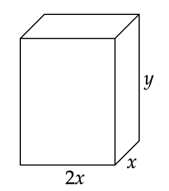
Zauważ, że krawędź prostopadłościanu musi być dodatnia:
![]() .
.
Ze wzoru na objętość, czyli iloczyn trzech różnych krawędzi oblicz długość trzeciej z nich, czyli
![]() .
.
![]()
![]()
Z treści zadania wiesz, że suma długości wszystkich krawędzi prostopadłościanu musi być mniejsza od 28. Oblicz jakie wartości
![]() spełniają ten warunek.
spełniają ten warunek.
![]()
![]()
![]()
![]()
Skorzystaj ze schematu Hornera, aby obliczyć miejsca zerowe powyższej nierówności.
Narysuj tabelę. W pierwszym wierszu wpisz wszystkie kolejne współczynniki uporządkowanego wielomianu. W lewym dolnym rogu najniższego wiersza tabelki wpisz liczbę, która jest miejscem zerowym dwumianu, czyli 1. Przepisz pierwszy współczynniku bez zmian do dolnego wiersza. Tak otrzymaną liczbę 3 pomnóż przez liczbę 1, która jest miejscem zerowym dwumianu, następnie dodaj liczbę -7. Wynik będący liczbą -4 wpisz do kolejnej komórki dolnego wiersza w schemacie Hornera. Podobnie postępuj z kolejnymi współczynnikami wielomianu.
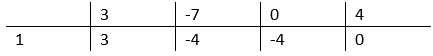
Liczby powstałe w dolnym wierszu są współczynnikami trójmianu, który powstał po dzieleniu. Zapisz go.
![]()
Oblicz rozwiązania drugiego nawiasu, czyli deltę i miejsca zerowe.
![]()
![]()
![]()
![]()
![]()
![]()
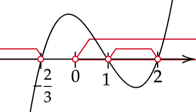
Zaznacz rozwiązania każdego z nawiasów na osi i zaznacz przedział, w którym funkcja jest pod osią. Pamiętaj o tym, że
![]() .
.
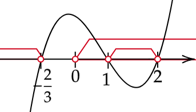
![]()
Zapisz pole całkowite prostopadłościanu. Zauważ, że powstanie funkcja zmiennej
![]() .
.
![]()
Oblicz pochodną funkcji
![]() .
.
![]()
Przyrównaj wartość pochodnej do zera i oblicz jej rozwiązania.
![]()
![]()
![]()
![]()
![]()
Zaznacz uzyskane miejsce zerowe na osi. Pamiętaj o uwzględnieniu dziedziny.
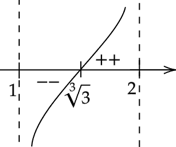
Oznacza to, że pochodna w przedziale
![]() ma jedno miejsce zerowe
ma jedno miejsce zerowe
![]() i zmienia w tym punkcie znak z ujemnego na dodatni. W takim razie funkcja
i zmienia w tym punkcie znak z ujemnego na dodatni. W takim razie funkcja
![]() maleje w przedziale
maleje w przedziale
![]() ,a rośnie w przedziale
,a rośnie w przedziale
![]() . Więc będzie do najmniejsza wartość pochodnej:
. Więc będzie do najmniejsza wartość pochodnej:
![]()
Oblicz długości pozostałych krawędzi prostopadłościanu.
![]()
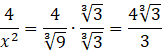
Oznacza to, że wymiary prostopadłościanu o najmniejszym polu całkowitym wynoszą
![]() .
.