Dany jest pewien równoległobok o bokach długości 4 i 6 cm oraz kącie ostrym miary 60°. Bryłę obrotową utworzono poprzez obrót tej figury wokół dłuższego boku równoległoboku. Oblicz objętość oraz pole powierzchni całkowitej tak powstałej bryły.
Naszkicuj sytuację przedstawioną w treści zadania:
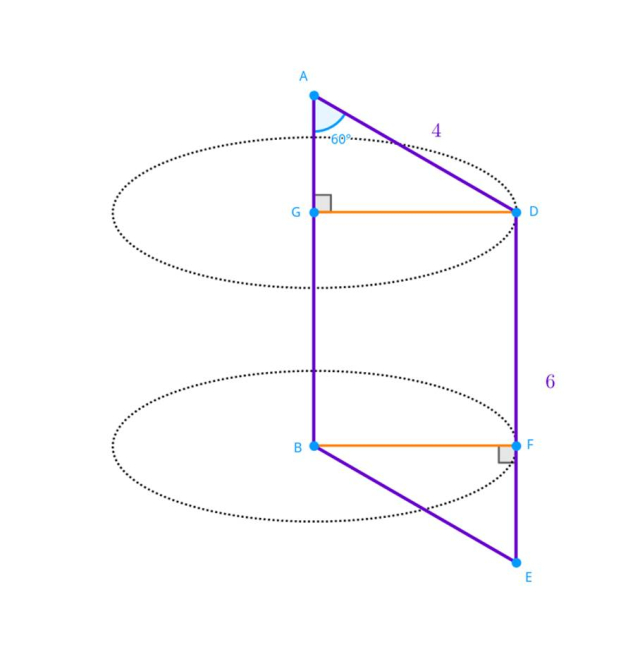
Oblicz długość odcinka AG:
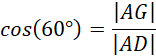
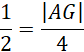
![]()
Oblicz długość odcinka GD:
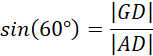
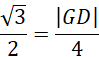
![]()
Na objętość bryły składa się: stożek AGD, walec GBFD oraz stożek wycięty z walca BEF:
![]()
![]()
![]()
Na pole powierzchni składają się: pole powierzchni bocznej utworzone przez krawędź DE i tworzące stożków: AD i BE:
![]()
![]()
![]()
Odp. Objętość bryły wynosi
![]() cm3, natomiast pole powierzchni całkowitej -
cm3, natomiast pole powierzchni całkowitej -
![]() cm2.
cm2.

Oblicz długości krawędzi w równoległoboku, korzystając z definicji funkcji trygonometrycznych w trójkącie prostokątnym, a następnie rozłóż utworzoną bryłę na składowe walce oraz stożki. Skorzystaj z odpowiednich wzorów na pola powierzchni bocznej i objętości walca i stożka.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
