Dany jest walec, którego powierzchnia boczna ma pole równe 120π cm2. Wyznacz jego objętość, jeśli promień jego podstawy jest o 7 cm krótszy od wysokości.
Oznaczenia:
r – promień podstawy walca
h – wysokość walca
Z treści zadania wiadomo:
![]()
Pole powierzchni bocznej:
![]()
![]()
![]()
![]()
![]()
![]()
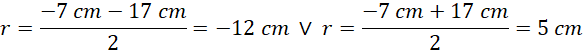
Z założeń geometrycznych promień musi być dodatni, zatem warunki zadania spełnia:
![]()
![]()
Wstaw te wartości do wzoru na objętość walca:
![]()

Wprowadź odpowiednie oznaczenia i zapisz zależność między wysokością a promieniem w postaci równości.
Rozpisz podane pole powierzchni bocznej ze wzoru na nią. Rozwiąż oba powstałe równania i wyznacz z nich promień podstawy walca oraz jego wysokość.
Oblicz szukaną objętość jako iloczyn pola podstawy i wysokości walca.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
