Dany jest pewien trapez prostokątny o podstawach długości 15 i 9 oraz kącie ostrym o mierze 45°. Bryłę obrotową utworzono, obracając figurę wokół krótszej podstawy. Oblicz objętość oraz pole powierzchni całkowitej utworzonej bryły.
Naszkicuj sytuację przedstawioną w treści zadania:

Odcinek GD ma długość:
![]()
Trójkąt AGD jest trójkątem prostokątnym równoramiennym, czyli:
![]()
Objętość bryły to suma objętości: walca ABCG i stożka wyciętego z walca AGD:
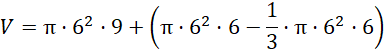
![]()
![]()
Pole powierzchni bocznej tworzą: koło o promieniu BC, wysokość walca CD i tworząca stożka AD:
![]()
![]()
![]()
Odp. Objętość bryły wynosi
![]() cm3, natomiast pole powierzchni -
cm3, natomiast pole powierzchni -
![]() cm2.
cm2.

Oblicz długości krawędzi w trapezie prostokątnym, korzystając z charakterystycznych długości boków w trójkącie prostokątnym równoramiennym, a następnie rozłóż utworzoną bryłę na składowe walce oraz stożki. Skorzystaj z odpowiednich wzorów na pola powierzchni bocznej i objętości walca i stożka.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
