Dany jest walec, w którym kąt pomiędzy przekątną d prostokąta będącego przekrojem osiowym walca, a podstawą tego walca, ma miarę α. Udowodnij, że poniższe wyrażenie opisuje jego objętość:
![]()
Oznaczenia:
r – promień podstawy walca
h – wysokość walca
Ogólny wzór na objętość walca:
![]()
Boki przekroju osiowego dowolnego walca pokrywają się z jego wysokością oraz średnicą podstawy.
Rysunek pomocniczy:
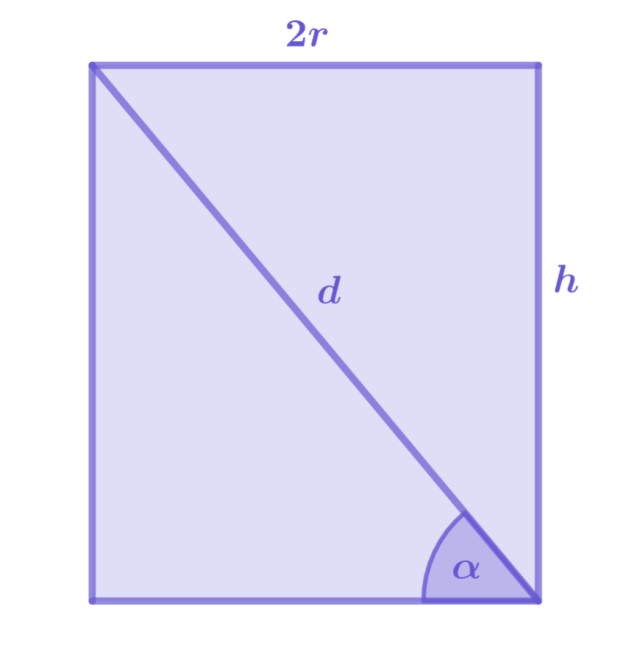
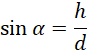
![]()
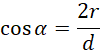
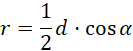
Wstaw te wartości do wzoru na objętość:
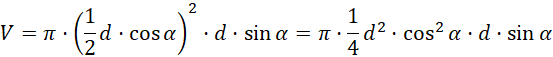
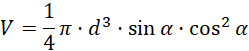
Co należało wykazać.

Wprowadź odpowiednie oznaczenia. Stwórz rysunek pomocniczy dotyczący przekroju osiowego walca.
Zapisz promień podstawy oraz wysokość walca przy pomocy odpowiednich funkcji trygonometrycznych oraz długości d.
Wstaw je do wzoru na objętość i zauważ, że otrzymane wyrażenie równa się temu w tezie, co kończy dowód.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
