Udowodnij, że objętość stożka opisanego na kuli w taki sposób, że jego wysokość jest dwa razy większa od średnicy kuli, jest dwa razy większa od objętości kuli.
Z:
V1 – Objętość stożka opisanego na kuli,
V2 – Objętość kuli.
T:
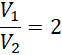
D:
Naszkicuj sytuację przedstawioną w treści zadania:
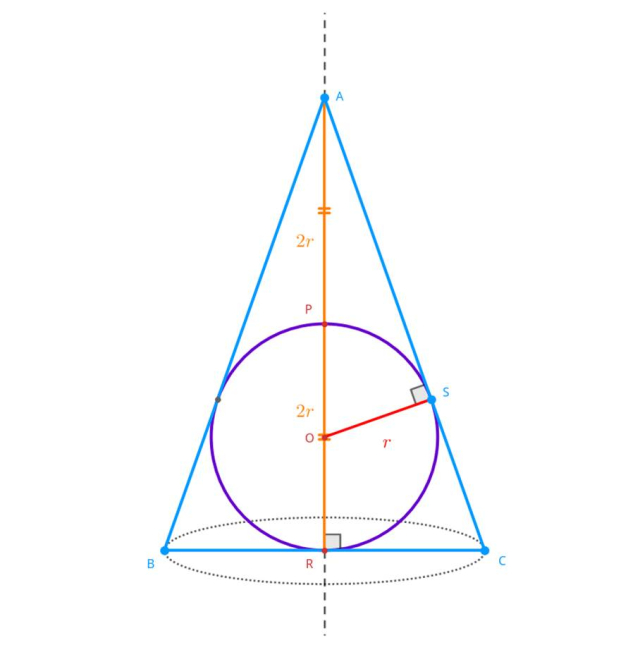
Zauważ, że trójkąty: OSA i CRA są podobne z zasady kąt-kąt-kąt. Oblicz długość odcinka SA:
![]()
![]()
![]()
Wykorzystaj to, by obliczyć promień podstawy RC:
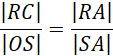
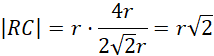
Oblicz objętość stożka:
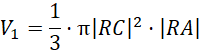
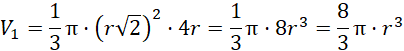
Oblicz objętość kuli:
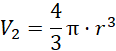
Wyznacz stosunek objętości:
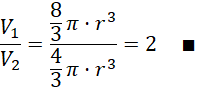

Wykorzystaj podobieństwo trójkątów oraz twierdzenie Pitagorasa, by wyznaczyć długość promienia podstawy stożka opisanego na kuli względem promienia tej kuli. Oblicz objętości brył korzystając z odpowiednich wzorów i porównaj je.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
