Dany jest walec, o objętości V i polu powierzchni bocznej P. Rozpatrz pewien kąt α pomiędzy przekątną prostokąta będącego jego przekrojem osiowym, a płaszczyzną podstawy. Udowodnij poniższą równość:
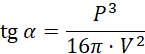
Oznaczenia:
r – promień podstawy walca
h – wysokość walca
Pole powierzchni bocznej:
![]()
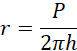
Objętość:
![]()
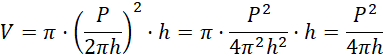
Stąd:
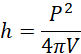
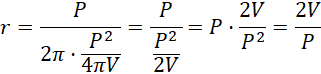
Boki przekroju osiowego dowolnego walca pokrywają się z jego wysokością oraz średnicą podstawy.
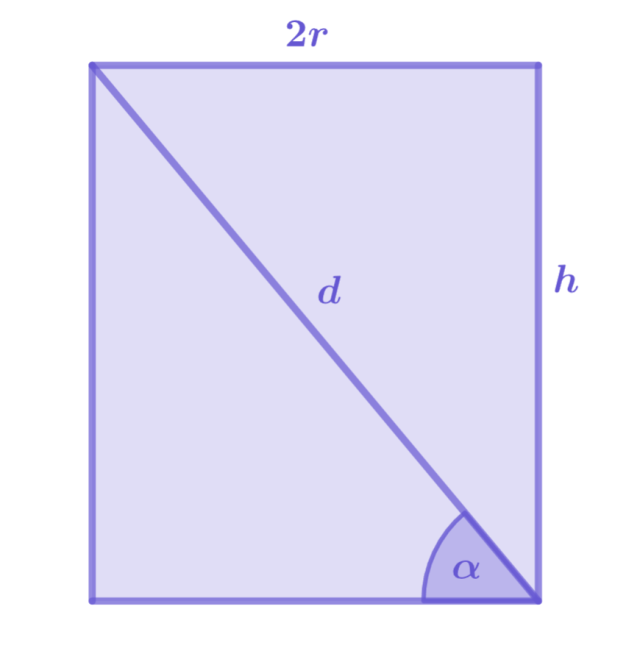
Rysunek pomocniczy:
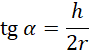
Wstaw wyznaczone wcześniej wartości:
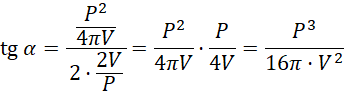
Co należało wykazać.

Wprowadź odpowiednie oznaczenia. Rozpisz pole powierzchni bocznej oraz objętość walca za pomocą odpowiednich wzorów i zapisz promień podstawy oraz wysokość walca z użyciem wyrażeń P i V.
Stwórz rysunek pomocniczy prezentujący przekrój osiowy walca.
Zapisz tangens rozpatrywanego kąta z użyciem wyznaczonych wcześniej wartości i zauważ, że otrzymane wyrażenie jest równe temu w tezie, co kończy dowód.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
