Dany jest stożek o promieniu podstawy i wysokości wynoszącym R. Rozpatrz przekrój tego stożka będący trójkątem o wierzchołku w wierzchołku stożka oraz podstawie będącej cięciwie odpowiadającej prostemu kątowi środkowemu w podstawie stożka. Wyznacz jego pole.
Oznaczenia:
R – wysokość i promień podstawy stożka
l – tworząca stożka
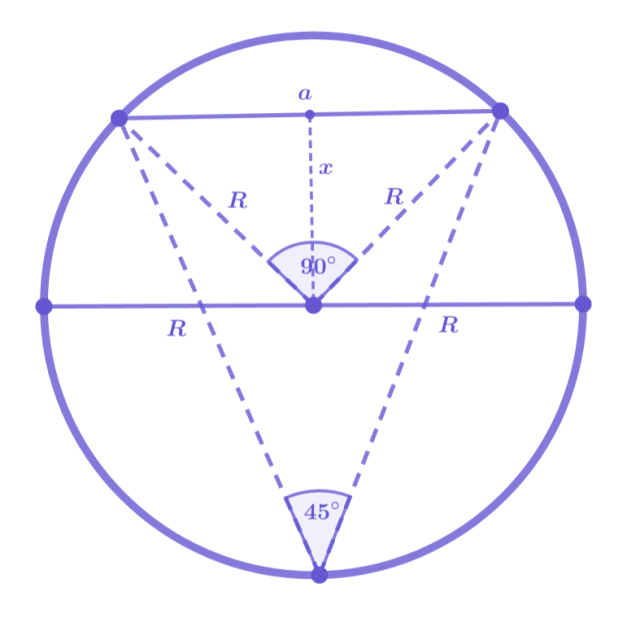
Rozpatrywana cięciwa a jest przeciwprostokątną w trójkącie prostokątnym równoramiennym, zatem:
![]()
Oblicz wartość x, która potrzebna będzie w kolejnym etapie zadania:
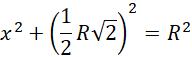
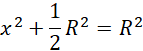
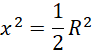
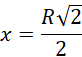
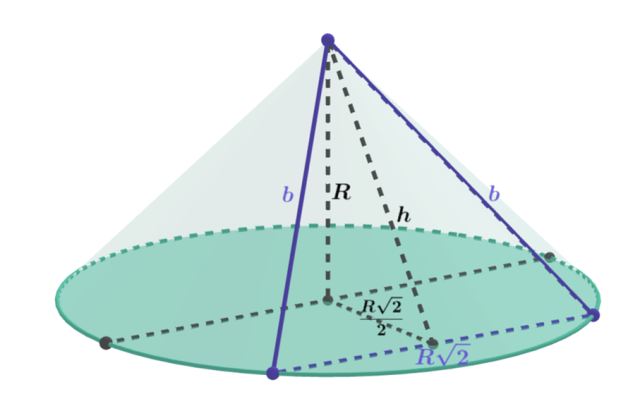
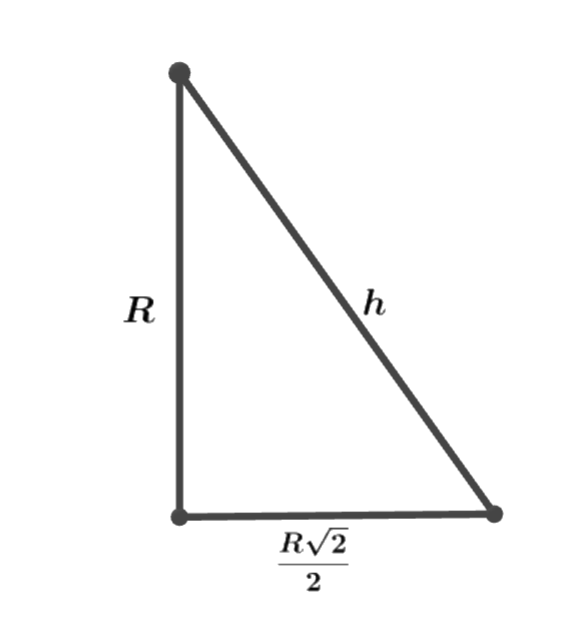
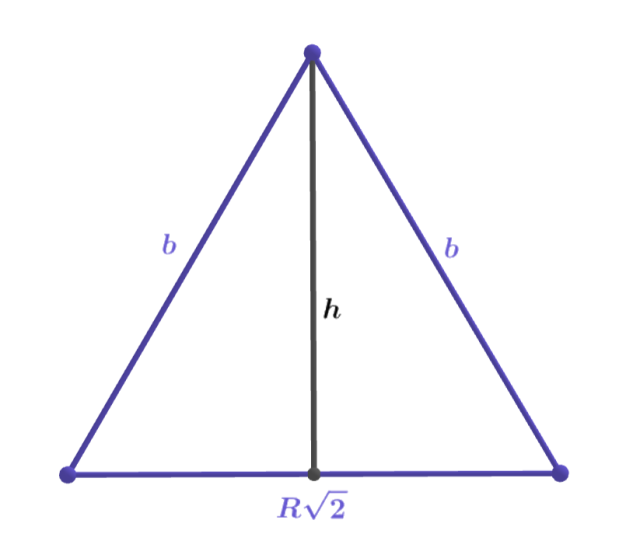
Bazując na powyższych rysunkach:
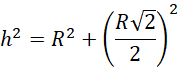
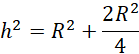
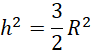
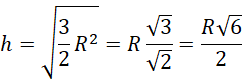
Rozpatrywany przekrój znajduje się na ostatnim rysunku, jego pole wynosi:
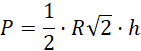
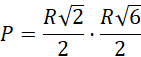
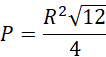
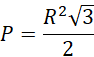

Stwórz odpowiednie rysunki pomocnicze.
Zauważ, że rozpatrywana średnica tworzy z promieniami podstawy trójkąt prostokątny równoramienny. Wyznacz jej długość.
Na rysunku całego stożka zaznacz rozpatrywany przekrój oraz znane już wartości. Oblicz brakującą wysokość przekroju korzystając z twierdzenia Pitagorasa.
Mając podstawę oraz wysokość trójkąta uzależnione od promienia R, wyznacz szukane pole.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
