Dana jest kula o środku w punkcie S. Na jej sferze leżą punkty A i B. Wyznacz jej pole powierzchni oraz objętość widząc, że:
![]()
![]()
Odcinki AS i BS są promieniami kuli (oznacz je jako r), ich długości są więc takie same. Trójkąt ABS jest więc równoramienny.
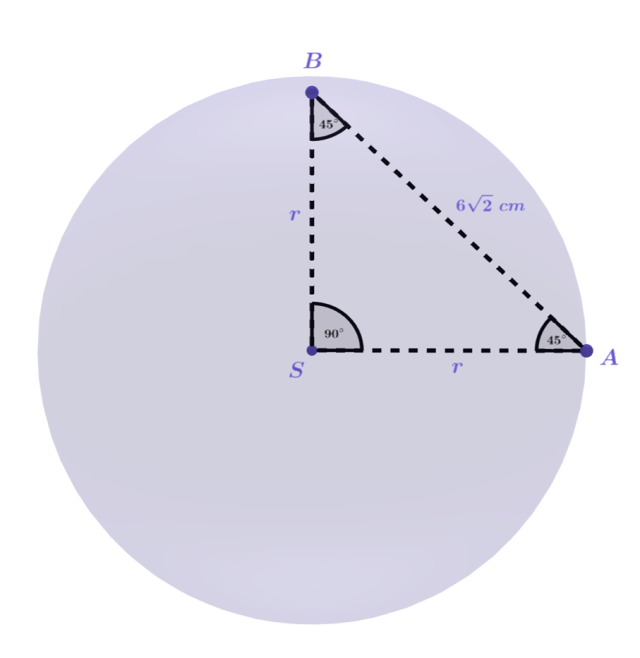
Z własności trójkąta o kątach 45°, 45°, 90°:
![]()
![]()
Pole powierzchni kuli:
![]()
Objętość kuli:
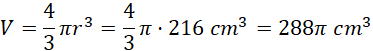

Stwórz rysunek pomocniczy.
Zauważ, że podane punkty tworzą trójkąt równoramienny o kątach 45°, 45°, 90°.
Z własności tego trójkąta wyznacz promień kuli i oblicz szukane pole oraz objętość ze wzorów:
![]()
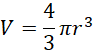

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
