O pewnym stożku wiadomo, że jego promień jest cztery razy krótszy od jego tworzącej. Wyznacz miarę wycinka koła będącego siatką płaszczyzny bocznej ostrosłupa.
Z treści zadania wynika, że:
![]()
Podstaw relację do wzoru na pole powierzchni bocznej ostrosłupa:
![]()
Oblicz pole koła o promieniu równym tworzącej stożka:
![]()
Oblicz miarę kąta środkowego wycinka koła:
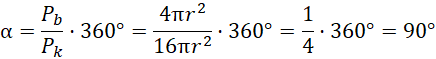

Oblicz pole powierzchni bocznej ostrosłupa i pole koła o promieniu równym tworzącej stożka, korzystając z relacji między długością promienia podstawy a tworzącą stożka. Iloraz tych pól to część pełnego koła, jaką zajmuje pole powierzchni bocznej. Pomnóż wynik przez 360°, by otrzymać wynik w stopniach.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
