O pewnym ostrosłupie wiadomo, że jego wysokość jest równa 21 cm, a pole podstawy wynosi 1350 cm2. Przez bryłę przeprowadzono płaszczyznę równoległą do płaszczyzny podstawy, która tworzy w bryle przekrój o polu 150 cm2. Oblicz odległość podstawy ostrosłupa do przekroju.

Oblicz stosunek długości fioletowych, przerywanych odcinków:
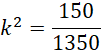
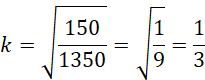
Oznacz odległość między płaszczyznami jako 𝑑. Wykorzystaj podobieństwo trójkątów:
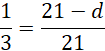
![]()
![]()
![]()
Odp. Odległość płaszczyzny przekroju od płaszczyzny podstawy jest równa 14 cm.

Skorzystaj z faktu, że pola powierzchni brył podobnych są podobne, jak kwadrat skali podobieństwa. Wykorzystaj wyznaczoną skalę oraz podobieństwo trójkątów, by wyliczyć odległość między płaszczyznami.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
