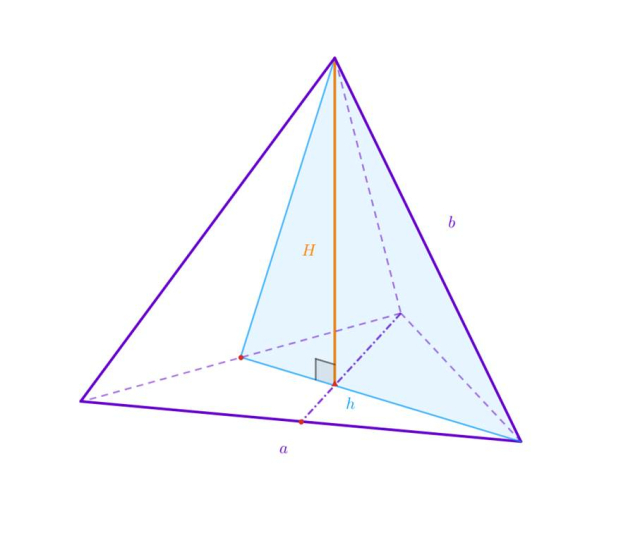
Oznacz długość krawędzi podstawy jako 𝑎, długość krawędzi bocznej jako 𝑏, wysokość podstawy jako ℎ oraz wysokość bryły jako 𝐻. Uzależnij długości tych krawędzi względem długości krawędzi podstawy:
![]()
![]()
Podstawa ostrosłupa to trójkąt równoboczny, zatem:
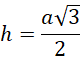
Oblicz wysokość bryły, korzystając z twierdzenia Pitagorasa:
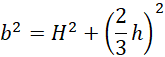
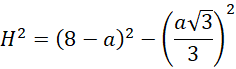
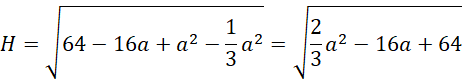
Wyznacz funkcję opisującą pole przekroju względem długości krawędzi podstawy:
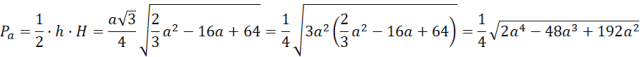
Wyznacz dziedzinę długości krawędzi podstawy:
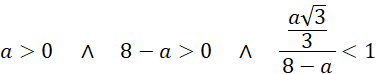
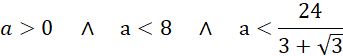
![]()
![]()
Wyznacz miejsce zerowe pochodnej tej funkcji. Zauważ, że pierwiastek jest funkcją monotonicznie rosnącą oraz ciągłą na przedziale danym przez funkcję (pole przekroju ostrosłupa jest zawsze dodatnie). Zatem:
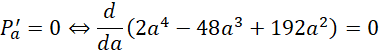
![]()
![]()
![]()
![]()
![]()
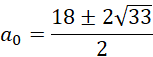
![]()
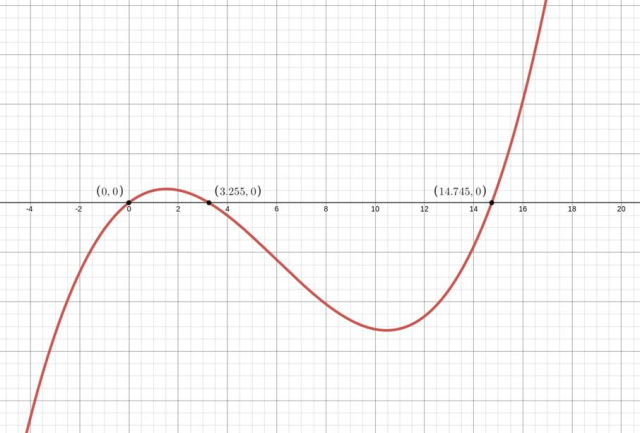
Pochodna zmienia znak z dodatniego na ujemny w wyznaczonym punkcie – masz do czynienia z maksimum lokalnym.
Odp. Długość krawędzi podstawy ostrosłupa o maksymalnym polu danego przekroju wynosi
![]() cm.
cm.

Oznacz krawędź podstawy, krawędź boczną, wysokość podstawy i bryły jako zmienne. Uzależnij długości tych zmiennych względem długości krawędzi podstawy. Podstaw otrzymane długości do wzoru na objętość ostrosłupa.
Trzeci warunek w dziedzinie funkcji opisującej objętość ostrosłupa to cosinus kąta między dwiema trzecimi wysokości podstawy i krawędzią boczną. Kąt między nimi musi być większy od zera (krawędź boczna nie może należeć do płaszczyzny podstawy), czyli cosinus musi być mniejszy od jeden.
Miejsca zerowe pochodnej wyznaczonej funkcji wskazują na prawdopodobne ekstrema lokalne. Sprawdź, czy pochodna zmienia znak dla wyznaczonej wartości – masz wtedy do czynienia z ekstremum lokalnym.
Sprawdź, czy obliczone miejsca zerowe pochodnej należą do dziedziny:
![]()
Dla drugiego miejsca zerowego:
![]()
![]()
![]()
![]()
![]()