Dany jest stożek o polu powierzchni całkowitej P oraz objętości V. Wiedząc, że pole trójkąta będącego jego przekrojem osiowym ma wartość 9
![]() cm2, a kąt rozwarcia ma miarę 120°, wyznacz P i V.
cm2, a kąt rozwarcia ma miarę 120°, wyznacz P i V.
Pole tego trójkąta jak podano w treści zadania to:
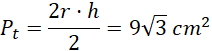
![]()
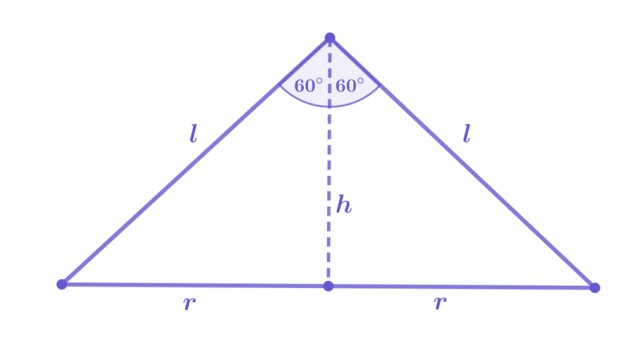
Z rysunku odczytaj:
![]()
![]()
![]()
Wstaw tę wartość do równania wyżej:
![]()
![]()
![]()
Zatem:
![]()
Z twierdzenia Pitagorasa:
![]()
![]()
![]()
Wstaw wyznaczone wartości do odpowiednich wzorów:
![]()
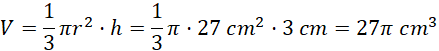

Stwórz rysunek pomocniczy. Korzystając z funkcji trygonometrycznych, twierdzenia Pitagorasa oraz podanego pola trójkąta, wyznacz promień, wysokość i długość tworzącej stożka.
Wstaw te wartości do wzorów na pole powierzchni całkowitej i objętość:
![]()
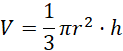

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
