Dana jest kula o promieniu długości 6 cm. Wpisano w nią ostrosłup prawidłowy trójkątny. Udowodnij, że wpisany ostrosłup osiąga maksymalną objętość, gdy jest on czworościanem foremnym o długości krawędzi
cm.
Z:
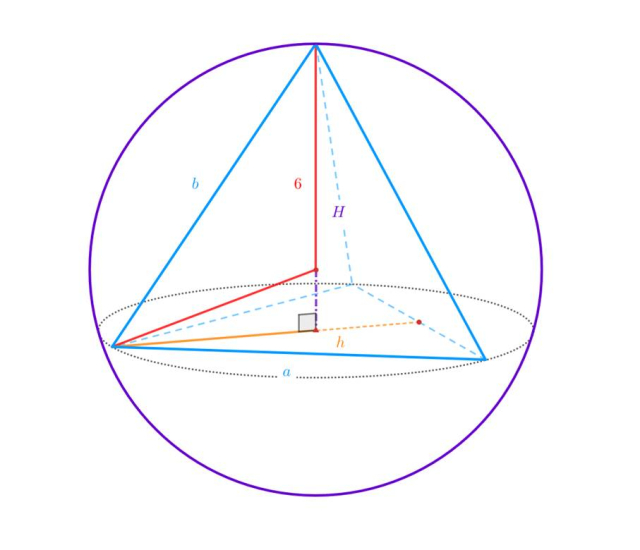
𝑎 – długość krawędzi podstawy ostrosłupa prawidłowego trójkątnego,
𝑏 – długość krawędzi bocznej ostrosłupa prawidłowego trójkątnego,
𝐻 – wysokość ostrosłupa prawidłowego trójkątnego,
ℎ - wysokość podstawy ostrosłupa prawidłowego trójkątnego.
T:
Dla ostrosłupa o maksymalnej objętości:
D:
Skoro podstawa ostrosłupa to trójkąt równoboczny, jego wysokość jest równa:
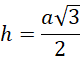
Spodek wysokości ostrosłupa prawidłowego trójkątnego pokrywa się ze środkiem przecięcia się wysokości, który dzieli te wysokości na odcinki o długościach w stosunku 2 : 1. To oznacza, że odległość wierzchołka podstawy od spodka wysokości jest równa:
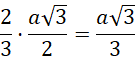
Wyznacz tę odległość względem wysokości ostrosłupa:
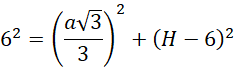
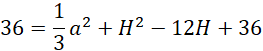
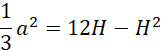
Wyznacz wzór na objętość ostrosłupa względem wysokości bryły:
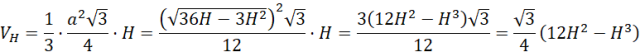
Wyznacz dziedzinę wysokości bryły:
Wyznacz miejsce zerowe pochodnej tej funkcji:
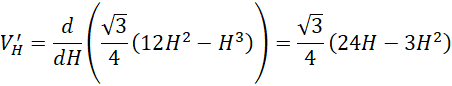
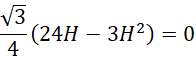
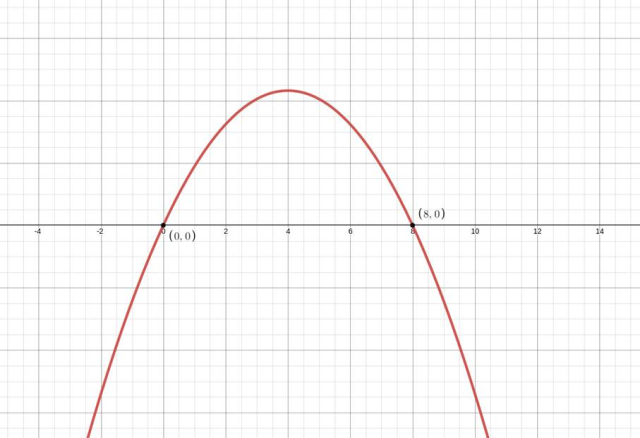
Pochodna zmienia znak z dodatniego na ujemny w wyznaczonym punkcie – masz do czynienia z maksimum lokalnym.
Oblicz długość krawędzi podstawy:
Oblicz długość krawędzi bocznej:
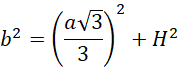
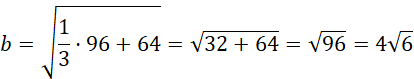
Ostrosłup jest prawidłowy, zatem jest to czworościan foremny:
Oznacz wysokość ostrosłupa oraz jego podstawy, długość krawędzi bocznej oraz krawędzi podstawy jako zmienne. Oblicz długości oznaczonych odcinków względem wysokości bryły i wyznacz przedział wartości. Podstaw otrzymane długości do wzoru na objętość ostrosłupa prawidłowego trójkątnego. Miejsca zerowe pochodnej wyznaczonej funkcji wskazują na prawdopodobne ekstrema lokalne. Sprawdź, czy pochodna zmienia znak dla wyznaczonej wartości – masz wtedy do czynienia z ekstremum lokalnym. Oblicz długości krawędzi ostrosłupa dla otrzymanej wysokości, korzystając z wyznaczonych wzorów. Sprawdź, czy ich długości są sobie równe.