Pewien ostrosłup o polu podstawy 150 cm2 przekrojono płaszczyzną równoległą do podstawy i odległą od niej na 14 cm. Pole powstałego przekroju jest równe 54 cm2. Wyznacz objętość całej bryły.
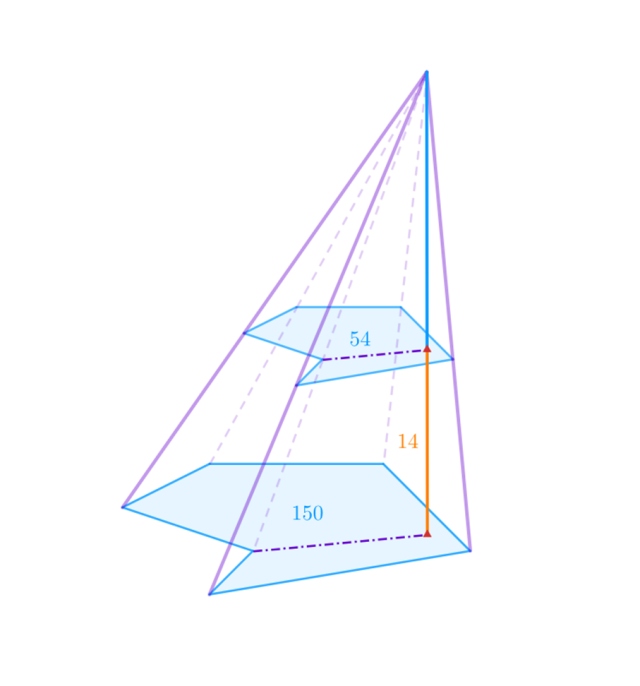
Oblicz stosunek długości fioletowych, przerywanych odcinków:
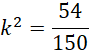
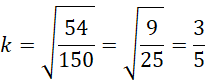
Oblicz wysokość niebieskiego odcinka, korzystając z podobieństwa trójkątów:
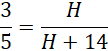
![]()
![]()
![]()
Wysokość całej bryły jest równa:
![]()
Objętość bryły jest równa:
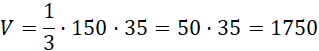
Odp. Objętość bryły wynosi 1750 cm3.

Skorzystaj z faktu, że pola powierzchni brył podobnych są podobne, jak kwadrat skali podobieństwa. Wykorzystaj wyznaczoną skalę oraz podobieństwo trójkątów, by wyliczyć wysokość mniejszego ostrosłupa. Oblicz objętość ostrosłupa, korzystając ze wzoru.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
