Dany jest pewien stożek, którego przekrój osiowy jest trójkątem równobocznym o polu
![]() cm2. W bryłę wpisano walec w taki sposób, że jedna jego podstawa zawiera się w podstawie stożka, a druga podstawa jest styczna całym okręgiem do powierzchni bocznej stożka. Wskaż wzór opisujący objętość wpisanego walca w zależności od promienia jego podstawy.
cm2. W bryłę wpisano walec w taki sposób, że jedna jego podstawa zawiera się w podstawie stożka, a druga podstawa jest styczna całym okręgiem do powierzchni bocznej stożka. Wskaż wzór opisujący objętość wpisanego walca w zależności od promienia jego podstawy.
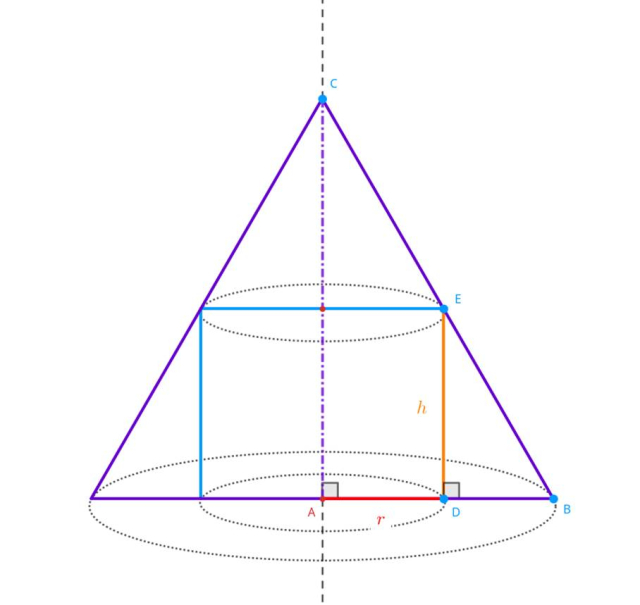
Opisz promień wpisanego walca jako 𝑟 i wysokość jako ℎ. Oblicz długość boku przekroju osiowego stożka:
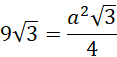
![]()
![]()
Długość odcinka AB to połowa długości boku trójkąta równobocznego, a więc:
![]()
Długość odcinka DB wynosi:
![]()
Uzależnij wysokość walca od długości promienia podstawy:
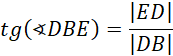
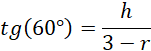
![]()
Długość promienia nie może przekraczać połowy długości boku przekroju, czyli:
![]()
Wyznacz wzór na objętość walca względem długości promienia podstawy:
![]()

Oznacz promień podstawy walca oraz jego wysokość jako zmienne. Oblicz długość boku przekroju, a następnie wysokość walca względem długości promienia podstawy. Podstaw otrzymane długości do wzoru na objętość ostrosłupa i wyznacz dziedzinę.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
