Dany jest walec o promieniu podstawy r. Na jego górnej podstawie wybrano pewien dowolny punkt A. Punkt ten wraz z osią walca tworzy płaszczyznę, która jest prostopadła do przekroju osiowego. Kąt ostry α równy jest kątowi BAC.
Na podstawie tych informacji wyznacz wysokość walca.
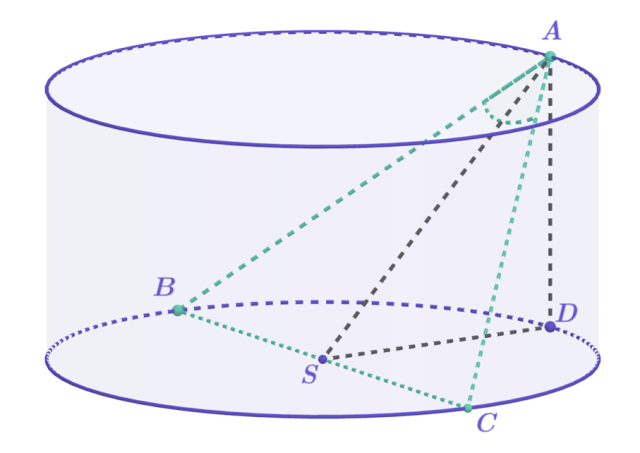
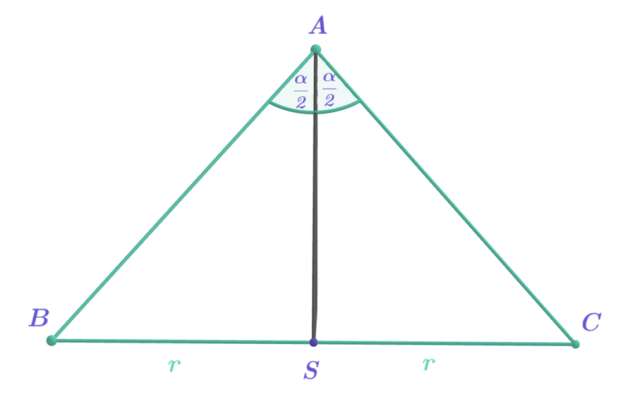

h – szukana wysokość
Z rysunku drugiego:
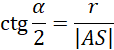
![]()
Z rysunku trzeciego oraz twierdzenia Pitagorasa:
![]()
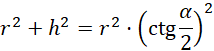
![]()
![]()
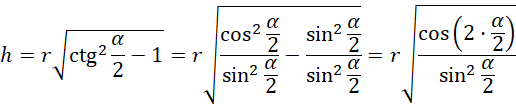
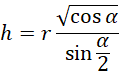

Wykonaj odpowiedni rysunek pomocniczy. Zwróć uwagę, że punkt A leży na okręgu, a średnica BC jest prostopadła do płaszczyzny utworzonej przez punkt A i oś walca.
Uzależnij jeden z brakujących boków od promienia r oraz funkcji cotangens połowy kąta α.
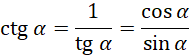
Ułóż równanie korzystając z twierdzenia Pitagorasa i wyznaczonych wartości. Oblicz z niego szukaną wysokość. Przy rozwiązywaniu wykorzystaj tożsamość trygonometryczną:
![]()

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
