O pewnym stożku wiadomo, że jego promień jest cztery razy krótszy od jego tworzącej. Wyznacz sinus kąta rozwarcia stożka. Skorzystaj ze wzoru
![]() .
.
Z treści zadania oraz podpunktu b) wynika, że:
![]()
![]()
Oblicz sinus oraz cosinus połowy kąta rozwarcia stożka:
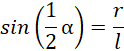
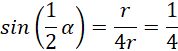
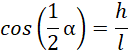
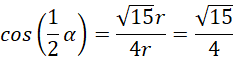
Skorzystaj z zaproponowanego wzoru:
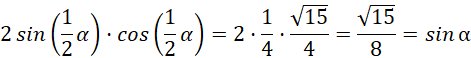

Zauważ, że wysokość opuszczona na średnicę podstawy przekroju osiowego stożka wyznacza dwa przystające trójkąty prostokątne. Kąt rozwarcia przekroju jest podzielony na pół pomiędzy te trójkąty. Oblicz sinus i cosinus połowy kąta, korzystając z definicji funkcji trygonometrycznych w trójkącie prostokątnym, a następnie skorzystaj ze wzoru
![]() .
.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
