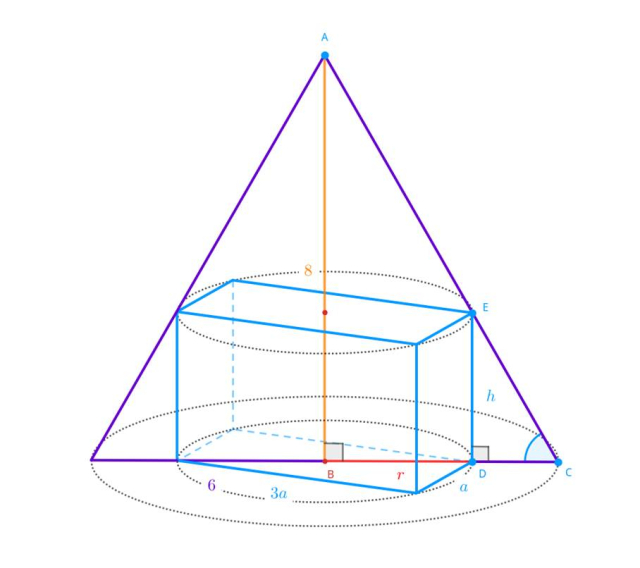
Oznacz krawędzi wpisanego prostopadłościanu jako 𝑎, 3𝑎 i ℎ. Promień okręgu opisanego na podstawie prostopadłościanu będący jednocześnie połową przekątnej podstawy oznacz jako 𝑟.
Uzależnij wymiary prostopadłościanu od długości krawędzi krótszej podstawy:
![]()
![]()
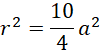
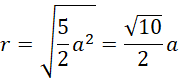
Skoro długość promienia podstawy stożka wynosi 6, to długość odcinka DC jest równa:
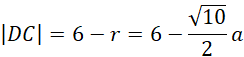
Uzależnij wysokość prostopadłościanu za pomocą definicji funkcji trygonometrycznych:
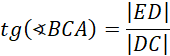
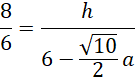
![]()
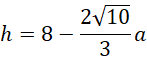
Wyznacz dziedzinę długości krawędzi prostopadłościanu:
![]()
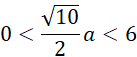
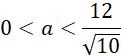
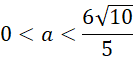
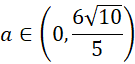
Wyznacz objętość prostopadłościanu względem długości krawędzi podstawy:
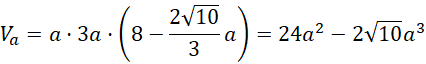
Wyznacz miejsce zerowe pochodnej tej funkcji:
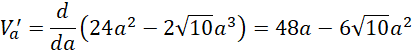
![]()
![]()
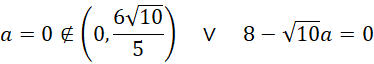
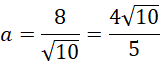
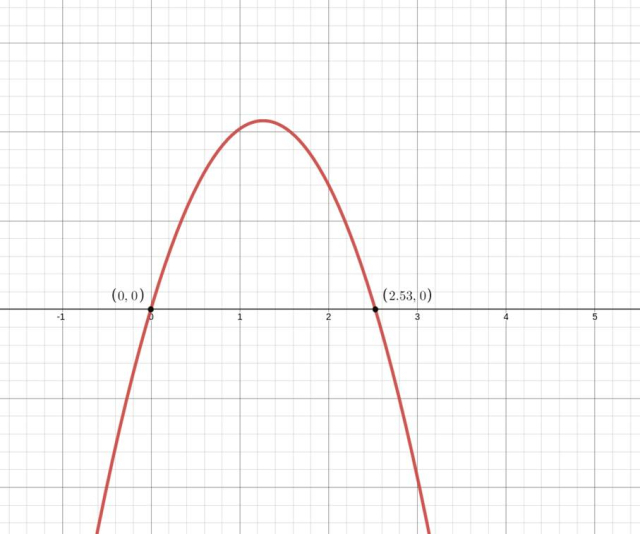
Pochodna zmienia znak z dodatniego na ujemny w wyznaczonym punkcie – masz do czynienia z maksimum lokalnym.
Oblicz długości krawędzi prostopadłościanu o maksymalnej objętości:
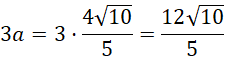
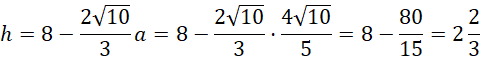
Odp. Wpisany prostopadłościan o maksymalnej objętości ma wymiary
![]() .
.

Oznacz krawędzie prostopadłościanu i promień okręgu opisanego na podstawie jako zmienne. Oblicz długości oznaczonych odcinków względem długości krótszego boku podstawy prostopadłościanu i wyznacz przedział wartości. Podstaw otrzymane długości do wzoru na objętość prostopadłościanu. Miejsca zerowe pochodnej wyznaczonej funkcji wskazują na prawdopodobne ekstrema lokalne. Sprawdź, czy pochodna zmienia znak dla wyznaczonej wartości – masz wtedy do czynienia z ekstremum lokalnym. Oblicz wymiary wpisanego prostopadłościanu dla otrzymanych wartości, korzystając z wyznaczonych wzorów.