Dana jest pewna kula wraz z wpisanym w nią sześcianem. Każdy z wierzchołków sześcianu należy do sfery danej kuli. Oblicz stosunek objętości tych brył.
Oznacz promień danej kuli jako 𝑅. Zauważ, że promień kuli to połowa przekątnej bryły sześcianu. O długości przekątnej sześcianu wiadomo, że:
![]()
gdzie 𝑎 to długość krawędzi sześcianu. Mamy więc:
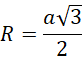
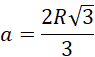
Objętość sześcianu jest równa:
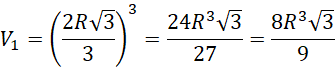
Objętość kuli jest równa:
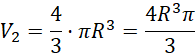
Stosunek objętości jest równy:
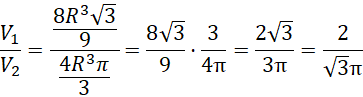
Odp. Stosunek objętości kuli do sześcianu jest równy
![]() : 2.
: 2.

Zauważ, że promień kuli opisanej w ten sposób na sześcianie określa połowę przekątnej bryły sześcianu. Podstaw odpowiednie długości do wzorów na objętości sześcianu oraz kuli.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
