Jeden z punktów na brzegu koła jest jednocześnie końcem cięciwy długości 20 cm oraz średnicy długości 29 cm. Poprzez obrót tej cięciwy wokół średnicy powstaje pewna bryła. Wyznacz pole jej całkowitej powierzchni.
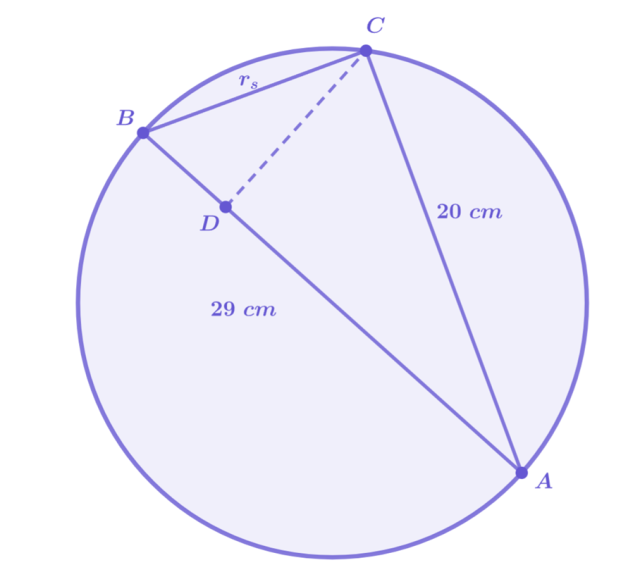
W wyniku rozpatrywanego obrotu powstaje sama powierzchnia boczna stożka o promieniu długości |CD|, wysokości |AD| i tworzącej |AC|.
Zauważ, że kąt ACB oparty jest na średnicy, jest to więc kąt prosty. Zatem:
![]()
![]()
![]()
![]()
Korzystając z twierdzenia Pitagorasa ułóż układ:
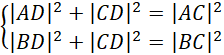
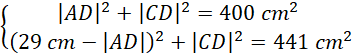
Od drugiego równania odejmij pierwsze, dla wygody rozwiązywania pomiń na razie jednostki.
![]()
![]()
![]()
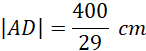
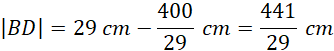
Długość boku CD oblicz ze wzoru:
![]()
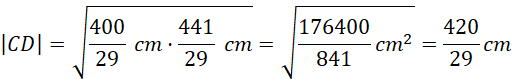
Mając wszystkie potrzebne dane wstaw je do wzoru na pole powierzchni bocznej stożka:
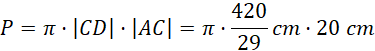
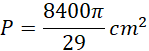

Stwórz rysunek pomocniczy. Zauważ, że bryłą powstałą w wyniku rozpatrywanego obrotu będzie powierzchnia boczna stożka.
Wyznacz długość jego promienia oraz tworzącej korzystając z twierdzenia Pitagorasa, wzoru na wysokość wychodzącą z kąta prostego.
Szukane pole oblicz ze wzoru na pole powierzchni bocznej stożka:
![]()

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
