Dane są dwie styczne zewnętrznie do siebie kule o których wiadomo, że jedna ma objętość 27 razy większą od drugiej. Opisano na nich stożek (podstawa styczna do większej kuli, okręgi kul należą do powierzchni bocznej stożka). Udowodnij, że kąt między ramionami przekroju osiowego stożka jest równy 60°.
Z:
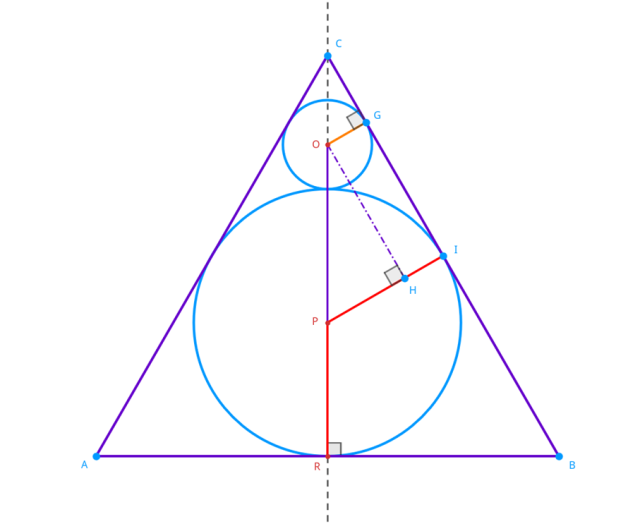
ABC – Trójkąt będący przekrojem osiowym,
r – Długość promienia mniejszej kuli
T:
![]()
D:
O objętościach kul wiadomo, że objętość większej z nich jest 27 razy większa od drugiej. Wyznacz skalę podobieństwa brył:
![]()
![]()
Zatem gdy odcinek OG ma długość 𝑟, odcinek PI ma długość 3𝑟. Jako że odcinek OP zawiera oba promienie kul, to jego długość wynosi 4𝑟.
Zauważ, że trójkąty ACR i CRB są przystające. Trójkąty COG, CPI i OPH są podobne. Oblicz miarę kąta POH, korzystając z definicji funkcji trygonometrycznych:
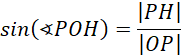
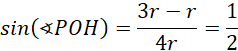
![]()
Skoro trójkąty są podobne, to kąt OCG również ma miarę 30°. Ponieważ trójkąty są przystające, to miara kąta ACB to suma miar kątów ACR i RCB. A to daje:
![]()

Skorzystaj z podobieństwa kul i stosunku ich objętości, by obliczyć stosunek ich promieni (objętości brył podobnych są podobne, jak sześcian skali podobieństwa). Wyznacz pary trójkątów podobnych w przekroju osiowym, a następnie skorzystaj z definicji funkcji trygonometrycznych, by określić miarę kąta odpowiadającego połowie szukanego kąta.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
