Poprzez obrót trójkąta prostokątnego o przeciwprostokątnej 25 cm (których stosunek długości przyprostokątnych to 4 : 3) wokół krótszej z przyprostokątnych, powstaje stożek. Wyznacz jego objętość.
Oznacz przyprostokątne jako: 3a, 4a.
![]()
![]()
![]()
![]()
![]()
Przyprostokątne mają więc długości: 15 cm i 20 cm.
W wyniku rozpatrywanego obrotu wysokość h otrzymanego stożka będzie wynosić 15 cm, a promień r jego podstawy 20 cm.
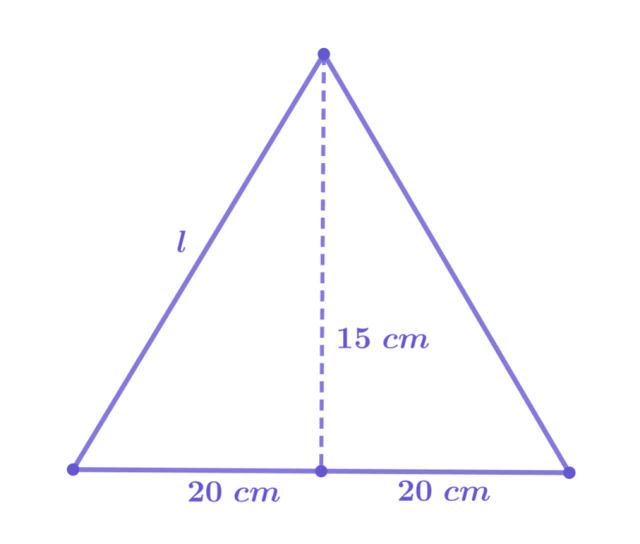
![]()
![]()
![]()
Wstaw znalezione wartości do wzoru na objętość stożka:
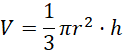
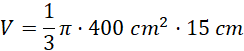
![]()

Wyznacz długości przyprostokątnych danego trójkąta. Przeanalizuj podany obrót i zauważ, jaka będzie wysokość i promień podstawy powstałego stożka.
Oblicz objętość danego stożka korzystając ze wzoru:
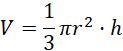

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
