Dany jest pewien stożek. Jego przekrój osiowy ma pole 9 dm2, natomiast miara kąta między ramionami przekroju wynosi 150°. Udowodnij, że objętość bryły wynosi
dm3.
T:
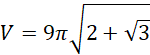
D:
Oblicz długość tworzącej stożka:
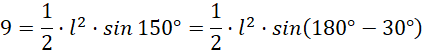
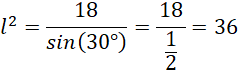
Oblicz długość średnicy podstawy:
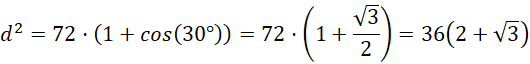
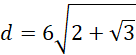
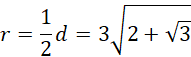
Oblicz wysokość stożka:
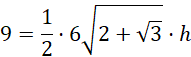
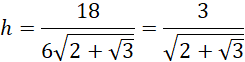
Oblicz objętość stożka:
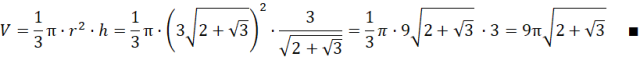
Zauważ, że przekrój stożka jest trójkątem równoramiennym, którego znane jest pole oraz miara kąta między ramionami. Skorzystaj ze wzoru na pole trójkąta:
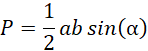
gdzie 𝑎 i 𝑏 to długości ramion z kątem α rozpostartym między nimi. Posłuż się wzorami redukcyjnymi, by wyznaczyć wartość sinusa kąta.
Wykorzystaj twierdzenie cosinusów, by obliczyć długość podstawy przekroju – średnicy podstawy stożka:
gdzie 𝑎, 𝑏 i 𝑐 to boki pewnego trójkąta, natomiast kąt α leży naprzeciw boku 𝑎. Tutaj również wykorzystaj wzór redukcyjny dla cosinusa kąta.
Znając długość promienia podstawy, oblicz wysokość stożka za pomocą twierdzenia Pitagorasa. Podstaw obliczone długości do wzoru na objętość stożka i skonfrontuj otrzymaną wartość z postawioną tezą.