W pewien stożek wpisano walec – jedna jego podstawa należy do podstawy stożka, a druga jest styczna całym okręgiem do powierzchni bocznej stożka. Wiedząc, że promień podstawy stożka jest dwa razy większy od promienia podstawy walca, oblicz stosunek objętości walca do całego stożka.
Oznacz objętość całego stożka jako 𝑉. Wiedząc, że skala podobieństwa stożka o podstawie z podstawy walca do całego stożka wynosi
![]() , objętość mniejszego stożka wynosi:
, objętość mniejszego stożka wynosi:
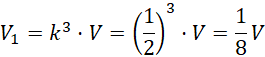
Zauważ, że skoro skala podobieństwa wynosi
![]() , to podstawa walca dzieli wysokość na dwie równe części. Zatem walec i mniejszy stożek mają tę samą podstawę oraz wysokość, czyli objętość walca jest trzy razy większa od objętości tego stożka:
, to podstawa walca dzieli wysokość na dwie równe części. Zatem walec i mniejszy stożek mają tę samą podstawę oraz wysokość, czyli objętość walca jest trzy razy większa od objętości tego stożka:
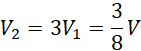
Odp. Objętość walca to
![]() objętości całego stożka.
objętości całego stożka.

Wykorzystaj podobieństwo brył (objętości brył podobnych są podobne jak sześcian skali podobieństwa), by obliczyć stosunek objętości stożka o podstawie z podstawy walca do objętości całego walca. Zauważ, że wysokość oraz podstawa walca i stożka są takie same, zatem objętość walca:
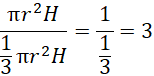
jest trzy razy większa od objętości stożka.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
