Dany jest walec, którego koło w podstawie ma obwód 6π cm. Wyznacz jego objętość oraz pole całkowitej powierzchni wiedząc, że jeśli rozwinąć jego powierzchnię boczną, to kąt pomiędzy przekątną otrzymanego prostokąta, a bokiem równym wysokości walca ma miarę 30°.
Oznaczenia:
r – promień podstawy walca
h – wysokość walca
Obwód podstawy:
![]()
![]()
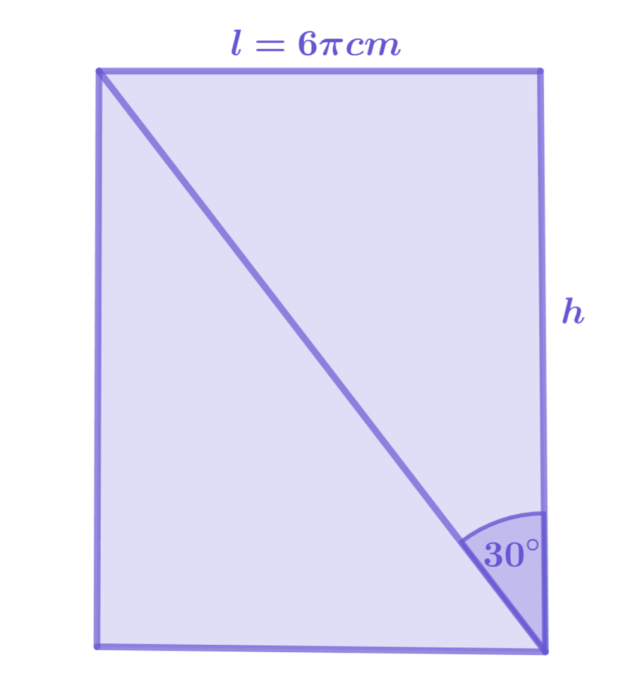
Obwód l jest jednocześnie jednym z boków prostokąta będącego powierzchnią boczną walca.
Stwórz rysunek pomocniczy:
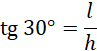
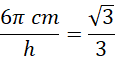
![]()
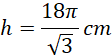
![]()
Oblicz pole powierzchni całkowitej i objętość z odpowiednich wzorów:
![]()
![]()
![]()
![]()

Oblicz promień podstawy walca mając podany obwód. Zauważ, że obwód ten jest jednocześnie jednym z boków prostokąta będącego powierzchnią boczną walca.
Stwórz rysunek pomocniczy i wyznacz wysokość walca przy pomocy funkcji trygonometrycznych.
Oblicz szukane wielkości wstawiając promień podstawy i wysokość do odpowiednich wzorów.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
