O pewnym ostrosłupie prawidłowym czworokątnym wiadomo, że suma jego krawędzi wynosi 20. Wyprowadź wzór opisujący objętość tej bryły względem długości krawędzi podstawy.
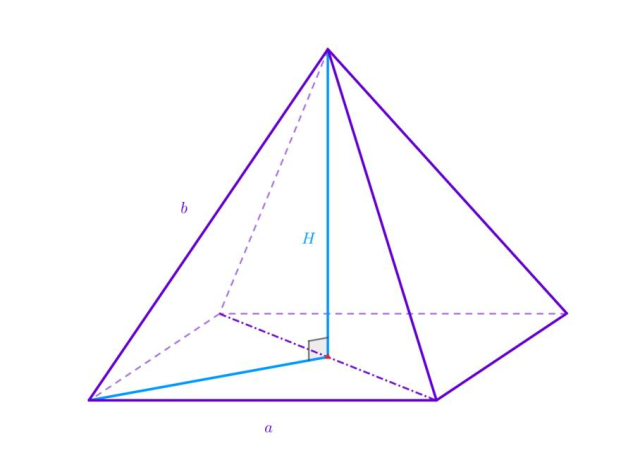
Uzależnij długość krawędzi bocznej od długości krawędzi podstawy:
![]()
![]()
Wyznacz wysokość ostrosłupa 𝐻:
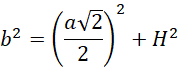
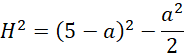
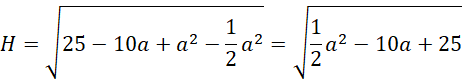
Wyznacz wzór na objętość ostrosłupa względem długości krawędzi podstawy bryły:
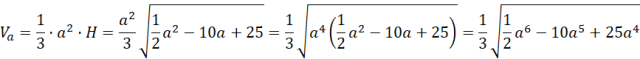
Wyznacz dziedzinę długości krawędzi podstawy:
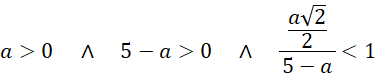
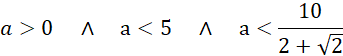
![]()
![]()

Oznacz krawędź podstawy oraz krawędź boczną jako zmienne. Oblicz wysokość oraz długość krawędzi bocznej względem długości krawędzi podstawy. Podstaw otrzymane długości do wzoru na objętość ostrosłupa.
Trzeci warunek w dziedzinie funkcji opisującej objętość ostrosłupa to cosinus kąta między połową przekątnej podstawy i krawędzią boczną. Kąt między nimi musi być większy od zera (krawędź boczna nie może należeć do płaszczyzny podstawy), czyli cosinus musi być mniejszy od jeden.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
