Dany jest pewien stożek o wysokości
![]() oraz promieniu podstawy równym 10. Sporządzono siatkę tego ostrosłupa. Wskaż kąt środkowy wycinka koła będącego powierzchnią ściany bryły:
oraz promieniu podstawy równym 10. Sporządzono siatkę tego ostrosłupa. Wskaż kąt środkowy wycinka koła będącego powierzchnią ściany bryły:
A. 180°
B. 210°
C. 240°
D. 300°
Oblicz długość tworzącej stożka:
![]()
![]()
Oblicz pole powierzchni bocznej tego stożka:
![]()
Oblicz pole koła o promieniu równym tworzącej ostrosłupa:
![]()
Miara kąta środkowego kąta wynosi:
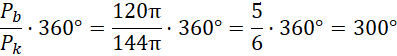
Odp. D.

Wyznacz długość tworzącej stożka za pomocą twierdzenia Pitagorasa (promień podstawy i wysokość to przyprostokątne trójkąta prostokątnego o przeciwprostokątnej o długości tworzącej stożka). Oblicz pole powierzchni bocznej stożka oraz pole koła o promieniu równym tworzącej stożka. Iloraz obu pól da stosunek pola powierzchni bocznej do pełnego koła. Pomnóż przez 360 by otrzymać wartość w stopniach.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
