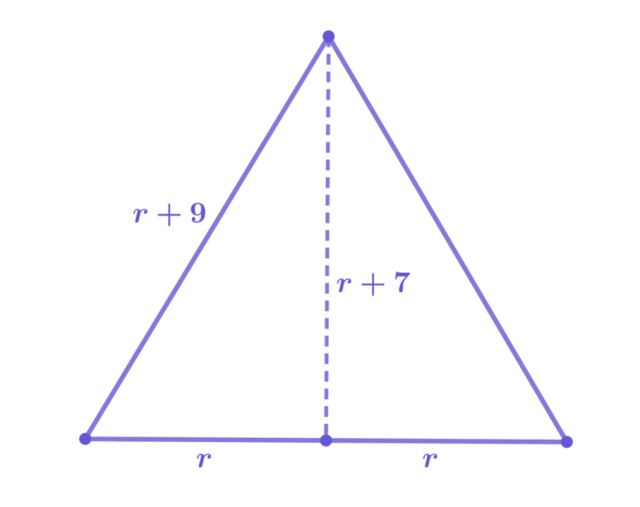
Dany jest stożek, w którym:
r – promień podstawy
h = r + 7 – wysokość
l = h + 2 – tworząca stożka
P – pole powierzchni całkowitej
V – objętość
Znajdź P i V.
![]()
![]()
![]()
![]()
![]()
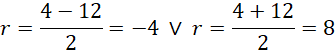
Z założeń geometrycznych promień jest dodatni, warunki zadania spełnia więc:
![]()
Zatem:
![]()
![]()
Pole powierzchni całkowitej:
![]()
Objętość:
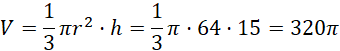

Bazując na danych z treści uzależnij długość tworzącej stożka od promienia jego podstawy.
Stwórz rysunek pomocniczy z przekrojem stożka i korzystając z twierdzenia Pitagorasa oblicz długość tworzącej stożka, promień podstawy oraz wysokość.
Szukane wielkości oblicz ze wzorów:
![]()
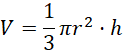

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
