Dany jest stożek o tworzącej 10 cm i polu całkowitej powierzchni 96π cm2. Wyznacz jego objętość.
Oznaczenia:
l = 10 cm – tworząca stożka
r – promień podstawy
h – wysokość
Pole powierzchni całkowitej stożka:
![]()
![]()
Dla wygody rozwiązywania pomiń na razie jednostki.
![]()
![]()
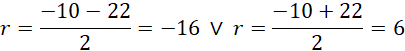
Z założeń geometrycznych promień r jest dodatni, zatem:
![]()
![]()
![]()
![]()
![]()
Wstaw wyznaczone wielkości do wzoru na objętość stożka:
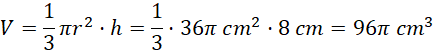

Rozpisz podane pole powierzchni całkowitej z odpowiedniego wzoru. Z otrzymanej równości wyznacz promień podstawy stożka.
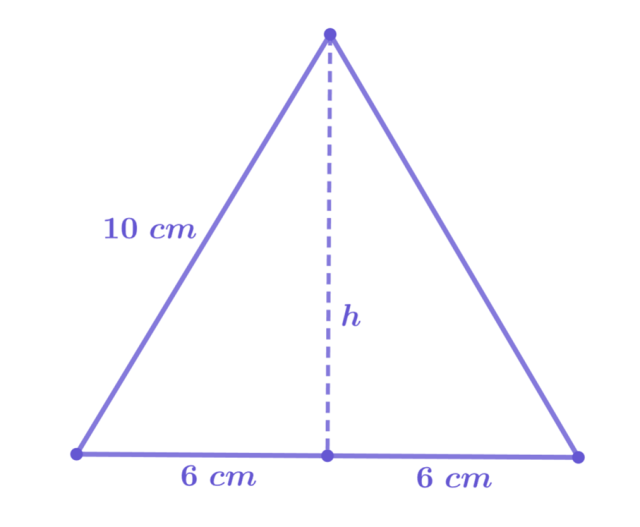
Brakującą wysokość oblicz korzystając z twierdzenia Pitagorasa.
Mając potrzebne dane wstaw je do wzoru na objętość stożka:
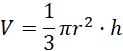

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
