Dany jest pewien stożek. Wiadomo o nim, że jego wysokość wynosi 24, a jego objętość to 800π. Wskaż długość tworzącej tego stożka:
A. 10
B. 25
C. 26
D. 30
Podstaw wartości pod wzór na objętość stożka, by obliczyć długość promienia podstawy:
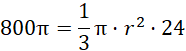
![]()
![]()
Zauważ, że wysokość stożka, promień podstawy oraz tworząca tworzą trójkąt prostokątny. Oblicz długość tworzącej:
![]()
![]()
Odp. C.

Podstaw wartości z treści zadania do wzoru na objętość ostrosłupa, aby wyznaczyć długość promienia podstawy:
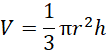
gdzie 𝑟 to promień podstawy stożka, a ℎ to jego wysokość.
Zauważ, że promień podstawy i wysokość stożka to przyprostokątne trójkąta prostokątnego o przeciwprostokątnej z tworzącej stożka. Wykorzystaj twierdzenie Pitagorasa, by obliczyć szukaną długość.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
