Dany jest walec o promieniu podstawy 5 cm i wysokości 6 cm. Punkty A i B leżą na okręgu kolejno górnej i dolnej podstawy, a |AB| = 10 cm. Rozpatrz odcinek pomiędzy o jednym końcu w AB, a drugim na osi obrotu walca. Znajdź długość najkrótszego z nich.
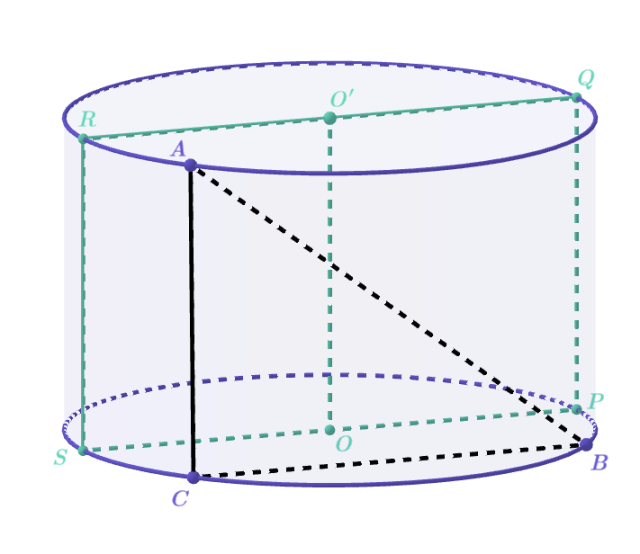
Rozpatrz dwie równoległe płaszczyzny: jedną zawierającą odcinek AB, drugą zawierającą oś walca.
Odległość między tymi płaszczyznami będzie jednocześnie szukaną w zadaniu odległością.
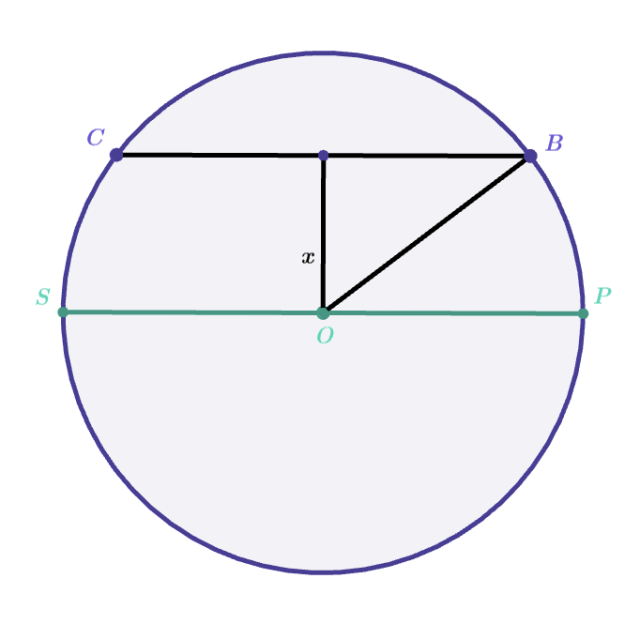
Szukaną wartością w zadaniu jest x.
Punkt O jest środkiem koła, zatem odcinek OB jest promieniem. |OB| = r.
Skorzystaj z rysunku pierwszego oraz twierdzenia Pitagorasa do obliczenia |BC|:
![]()
![]()
![]() – wysokość walca
– wysokość walca
![]()
![]()
Wracając do rysunku drugiego:
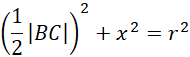
![]()
![]()
![]()

Wykonaj rysunek pomocniczy. Rozpatrz na nim dwie równoległe płaszczyzny: jedną zawierającą odcinek AB, a drugą zawierającą oś walca. Zauważ, że szukana w zadaniu odległość jest równa odległości między tymi płaszczyznami.
Korzystając z twierdzenia Pitagorasa wyznacz długość rzutu boku AB na dolną podstawę.
Następnie ponownie wykorzystując twierdzenie Pitagorasa oblicz szukaną odległość między płaszczyznami.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
