Dany jest pewien walec, o którym wiadomo, że jego objętość to 5π dm3, natomiast pole powierzchni całkowitej - 13π dm2. Oblicz promień podstawy bryły.
Z treści zadania wiadomo, że:
![]()
Uzależnij wysokość walca od promienia podstawy za pomocą jednego z równań:
![]()
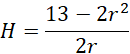
Podstaw wartość do drugiego równania:
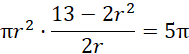
![]()
![]()
Zauważ, że pierwiastkiem wielomianu stopnia trzeciego jest 𝑟 = 2:
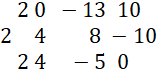
![]()
Oblicz miejsca zerowe wielomianu stopnia drugiego:
![]()
![]()
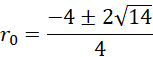
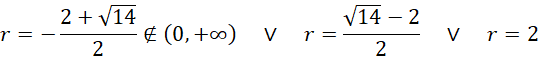
Odp. Długość promienia podstawy tego walca jest równa 2 dm lub
![]() dm.
dm.

Wykorzystaj wzory na pole powierzchni całkowitej i objętość walca, by uzależnić wysokość bryły od jej promienia podstawy. Wstaw obliczoną zależność do jednego ze wzorów by otrzymać równanie wielomianowe stopnia trzeciego opisujące wszystkie możliwe długości promienia podstawy walca, spełniające założenia zadania. Wykorzystaj schemat Hornera, by rozłożyć wielomian na iloczyn wielomianów niższego stopnia, a następnie rozwiąż je.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
