W pewien stożek wpisano walec – jedna jego podstawa należy do podstawy stożka, a druga jest styczna całym okręgiem do powierzchni bocznej stożka. Podstawa stożka i walca wyznaczają razem podstawy pewnego stożka ściętego. Wiedząc, że stosunek promienia podstawy walca do promienia podstawy stożka wynosi 3 : 2, oblicz stosunek różnicy objętości tego stożka ściętego oraz walca do całego stożka.
Odczytaj skalę podobieństwa stożka wyznaczonego przez podstawę walca do całego stożka:
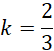
Oznacz objętość całego stożka jako 𝑉. Oblicz objętość stożka wyznaczonego przez podstawę walca:
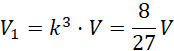
Zauważ, że skala podobieństwa dotyczy wysokości brył. Po oznaczeniu wysokości całego stożka jako 𝐻, wysokość mniejszego, podobnego stożka wynosi
![]() , natomiast walca -
, natomiast walca -
![]() . Pamiętając, że pole podstaw między badanymi bryłami jest takie same, porównaj ich wzory objętości:
. Pamiętając, że pole podstaw między badanymi bryłami jest takie same, porównaj ich wzory objętości:
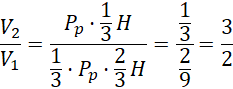
Zatem objętość walca względem objętości całego stożka wynosi:
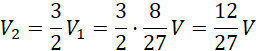
Poszukiwana objętość to różnica całego stożka i sumy objętości walca i mniejszego stożka:
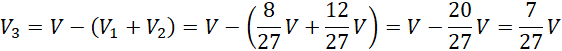
Odp. Stosunek różnicy objętości stożka ściętego i walca do całego stożka wynosi
![]() .
.

Odczytaj skalę podobieństwa brył. Wykorzystaj podobieństwo między stożkami, by policzyć stosunek ich objętości (objętości brył podobnych są podobne jak sześcian skali podobieństwa). Zauważ, że znany jest stosunek wysokości mniejszego stożka i walca. Podstaw do wzorów na objętości brył i porównaj, by poznać stosunek objętości mniejszego stożka do walca.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
