Aby obliczyć promień kuli wpisanej, skup się na przekroju ostrosłupa zawierającym wysokości przeciwległych ścian bocznych:
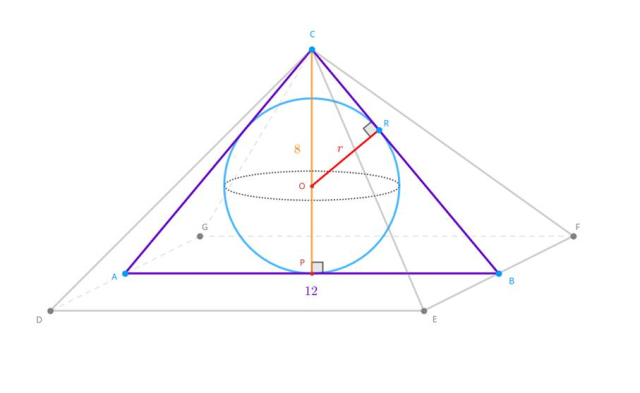
Spodek wysokości P dzieli odcinek AB na dwie równe części. Zatem długość odcinka PB wynosi 6. Oblicz długość odcinka CB:
![]()
![]()
Zauważ, że trójkąty COR i CBP są podobne (kąt-kąt-kąt). Oblicz więc długość promienia wpisanej kuli:
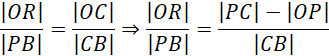
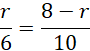
![]()
![]()
![]()
Aby obliczyć promień kuli opisanej, skup się na przekroju ostrosłupa zawierającym przeciwległe krawędzie boczne:
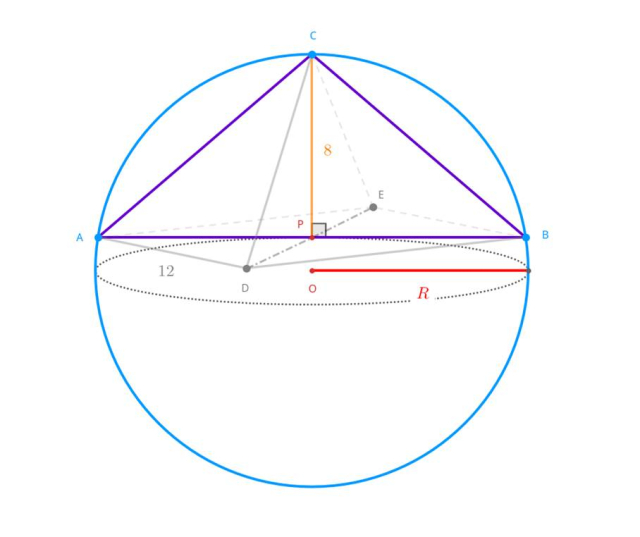
Odcinek AB to przekątna podstawy ADBE, która jest kwadratem. Długość odcinak AB wynosi zatem
![]() . Spodek wysokości P dzieli odcinek AB na dwie równe części. Zatem długość odcinka PB wynosi
. Spodek wysokości P dzieli odcinek AB na dwie równe części. Zatem długość odcinka PB wynosi
![]() .
.
Oblicz długość ramion przekroju:
![]()
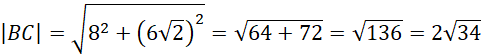
Oblicz pole przekroju:
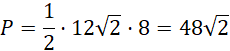
Wyznacz promień opisanej na bryle kuli:
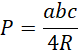
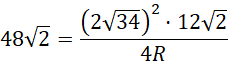
![]()
![]()
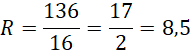
Odp. Promień kuli wpisanej ma długość 3 cm, a opisanej – 8,5 cm.

Znajdź odpowiednie przekroje, umożliwiające obliczenie szukanych promieni. Skorzystaj z twierdzenia Pitagorasa oraz podobieństwa figur, by odnaleźć długości potrzebnych odcinków. W przypadku promienia okręgu opisanego, oblicz pole przekroju na dwa sposoby, by skorzystać ze wzoru na pole trójkąta zawierającego promień okręgu opisanego na trójkącie.