Miasto A leży 20° szerokości geograficznej na północ od równika. Zakładając, że Ziemia jest idealną kulą, że jej promień jest równy 6300 km oraz że π to w przybliżeniu 3, wskaż odległość sferyczną od miasta A do równika:
A. 1050 km
B. 2100 km
C. 3150 km
D. 4200 km
Zauważ, że poszukiwana odległość to wycinek okręgu wielkiego kuli o kącie środkowym 20°, gdzie okrąg wielki zawiera miasto A oraz geograficzne bieguny globu. Oblicz długość tego wycinka:
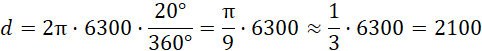
Odp. B.

Skorzystaj ze wzoru na wycinek okręgu o zadanym kącie:
![]()
gdzie 𝑟 to promień okręgu, a
![]() to kąt środkowy wycinka w stopniach.
to kąt środkowy wycinka w stopniach.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
