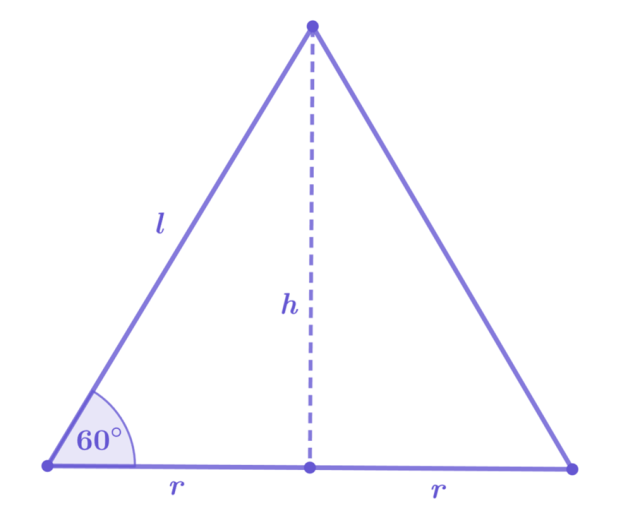
Dany jest stożek o polu powierzchni bocznej równym 50π cm2. Znajdź jego wysokość wiedząc, że kąt pomiędzy jego tworzącą a płaszczyzną podstawy ma miarę 60°.
![]()
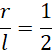
![]()
Pole powierzchni bocznej:
![]()
![]()
![]()
![]()
Z założeń geometrycznych promień jest zawsze dodatni, zatem:
![]()
![]()
Wróć do rysunku wyżej i skorzystaj z twierdzenia Pitagorasa:
![]()
![]()
![]()
![]()

Stwórz rysunek pomocniczy z przekrojem stożka. Korzystając z funkcji trygonometrycznych uzależnij tworzącą stożka od promienia.
Oblicz promień wstawiając wyznaczony stosunek do wzoru na pole powierzchni bocznej i rozwiązując powstałą równość.
Znajdź szukaną wysokość korzystając z twierdzenia Pitagorasa.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
