Pewna bryła powstaje w wyniku obrotu półkola o polu P wokół jego osi symetrii. Znajdź jej pole powierzchni całkowitej.
Niech średnica podanego półkola wynosi 2r, a promień r.
W wyniku rozpatrywanego obrotu powstanie półkula o promieniu r.
Ze wzoru na pole półkola:
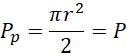
![]()
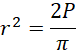
Pole powierzchni całkowitej półkuli będzie sumą jej sfery oraz pola koła w podstawie:
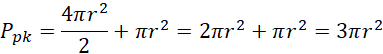
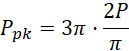
![]()

Zauważ, że w wyniku rozpatrywanego obrotu powstanie półkula, którego promień będzie taki sam jak promień podanego półkola.
Oblicz szukane pole wykorzystując poniższe wzory na pole półkola oraz pole powierzchni całkowitej półkuli:
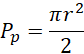
![]()

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
