![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
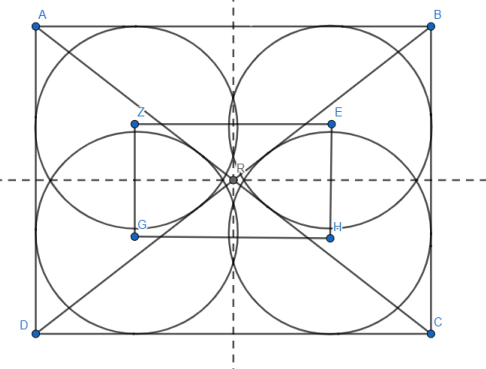
|ZG| = |AD| - 2r = 8 – 6 = 2
![]()
![]()

Poprowadź symetralne boków prostokąta. Następnie zauważ, że trójkąty ABC, BCD, CDA, DAB są trójkątami przystającymi. Promienie R okręgów wpisanych w te trójkąty mają takie same wartości. Zauważ, że odcinki ZE i GH oraz ZG i EH będą do siebie równoległe. Dzieje się tak dlatego, że punkty Z i E leżą na prostej równoległej do odcinka AB, a punkty G, H leżą na prostej równoległej do odcinka DC. Na podobnej zasadzie równoległe do siebie są odcinki EH i BC oraz ZG i AD. Sprawia to, że czworokąt ZEHG jest prostokątem. Zacznij od obliczenia długości przekątnej AC z twierdzenia Pitagorasa. Następnie oblicz pole trójkąta ABC, aby znaleźć długość promienia okręgu wpisanego w ten trójkąt. Oblicz długości boków prostokąta ZEGH i jego pole.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
