W kwadracie o boku długości 32 cm umieszczono trzy okręgi, które są styczne zewnętrznie oraz styczne do boków kwadratu. Okręgi styczne do tego samego boku kwadratu mają równe promienie. Oblicz promień każdego z tych okręgów.
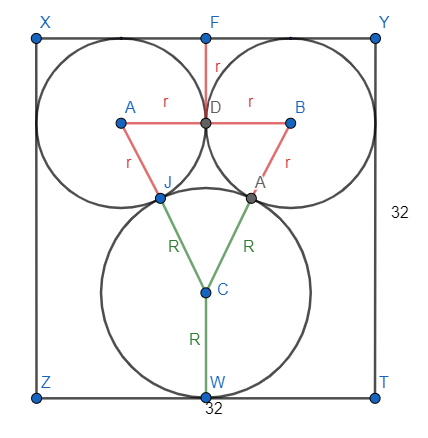
4r = 32 cm
r = 8 cm
|FD| + |DC| + |CW| = 32 cm
r + |DC| + R = 32 cm
![]()
Z tw. Pitagorasa w DBC
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Promienie okręgów mają 8 cm, 8 cm i 9 cm

Przyjmij oznaczenia jak na rysunku. Zauważ, że długość boku kwadratu jest równa długości 4 promieni r. Oblicz r. Następnie zauważ, że długość boku kwadratu jest równa sumie promienia r, promienia R i wysokości trójkąta ABC. Z tej równości wylicz długość |DC|. Kolejno skorzystaj z twierdzenia Pitagorasa w trójkącie DBC, podstaw wyliczoną wartość |DC|, za r podstaw 8 cm i wylicz wartość R.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
