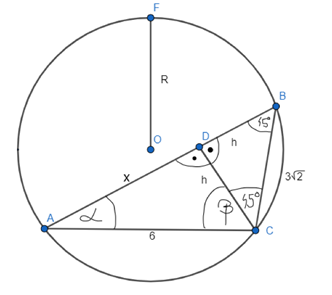
W trójkącie ABC, w którym |AC| = 6 i |BC| = 3√2, poprowadzono wysokość CD. Trójkąt BCD jest równoramienny. Oblicz miary kątów trójkąta ABC oraz promień okręgu opisanego na tym trójkącie.
![]()
![]()
Z tw. Pitagorasa w ADC
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
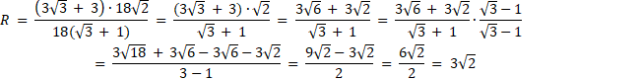
![]()

Trójkąt DBC jest trójkątem równoramienny prostokątnym, czyli kąty przy jego podstawie mają po
![]() . Skoro przeciwprostokątna tego trójkąta ma długość
. Skoro przeciwprostokątna tego trójkąta ma długość
![]() , to długości przyprostokątnych to 3. Oblicz długość x korzystając z twierdzenia Pitagorasa w trójkącie ADC. Następnie oblicz sinusa kąta
, to długości przyprostokątnych to 3. Oblicz długość x korzystając z twierdzenia Pitagorasa w trójkącie ADC. Następnie oblicz sinusa kąta
![]() , aby znaleźć miarę tego kąta. Kolejno znajdź miarę kąta
, aby znaleźć miarę tego kąta. Kolejno znajdź miarę kąta
![]() , korzystając z sumy miar kątów w trójkącie. Następnie oblicz pole trójkąta ABC. Następnie oblicz długość promienia okręgu opisanego na trójkącie ze wzoru
, korzystając z sumy miar kątów w trójkącie. Następnie oblicz pole trójkąta ABC. Następnie oblicz długość promienia okręgu opisanego na trójkącie ze wzoru
![]() , gdzie a,b i c to długości boków trójkąta.
, gdzie a,b i c to długości boków trójkąta.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
