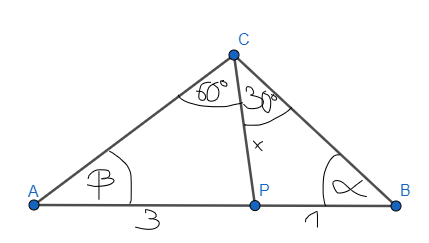
Na boku AB trójkąta ABC wybrano punkt P w taki sposób, że długość odcinka AP wynosi 3, długość odcinka BP wynosi 1, miara kąta ACP wynosi 60°, a miara kąta BCP wynosi 30°. Oblicz pole trójkąta ABC.
![]()
![]()
![]()
![]()
![]()
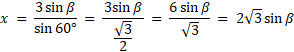
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Przyjmij oznaczenia jak na rysunku. Zacznij od wyznaczenia zależności kątów
![]() z sumy kątów w trójkącie. Oblicz długość x na dwa sposoby, z twierdzenia sinusów w trójkącie PBC i PCA. Przyrównaj te wartości do siebie i znajdź zależność
z sumy kątów w trójkącie. Oblicz długość x na dwa sposoby, z twierdzenia sinusów w trójkącie PBC i PCA. Przyrównaj te wartości do siebie i znajdź zależność
![]() . Podstaw za
. Podstaw za
![]() wartość
wartość
![]() .Oblicz tg
.Oblicz tg
![]() i wskaż wartość kątóIII.
i wskaż wartość kątóIII.
![]() . Następnie oblicz x i pole trójkąta. Oblicz miarę kąta CPB i zauważ, zę jest to kąt prosty, więc pole trójkąta można policzyć ze wzoru
. Następnie oblicz x i pole trójkąta. Oblicz miarę kąta CPB i zauważ, zę jest to kąt prosty, więc pole trójkąta można policzyć ze wzoru
![]()

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
