Mamy romb, w którym kąt ostry ma
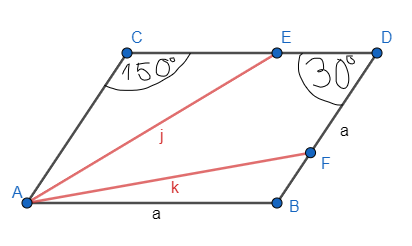
![]() , bok ma długość a i z wierzchołka kąta ostrego poprowadzono dwa odcinki (jak na rysunku), które podzieliły romb na trzy figury o identycznych polach. Wyznacz długości tych odcinków.
, bok ma długość a i z wierzchołka kąta ostrego poprowadzono dwa odcinki (jak na rysunku), które podzieliły romb na trzy figury o identycznych polach. Wyznacz długości tych odcinków.
![]()
![]()
![]()
Z przystawania trójkątów ACE i AFB
![]()
![]()
![]()
![]()
![]()
![]()
Z tw. cosinusów dla AFB
![]()
![]()
![]()
![]()
![]()
![]()

Figury ACE, EDFA i AFB mają równe pola. Porównując wzory na ich pola możesz dojść do równości |BF| = |CE|. Trójkąty te są przystające na podstawie cechy bkb (bok a, boki |BF| = |CE| i kąt
![]() ). Z ich przystawania wynika, że |AE| = |AF|, czyli j = k. Oblicz pole trójkąta AFB na dwa sposoby, jako
). Z ich przystawania wynika, że |AE| = |AF|, czyli j = k. Oblicz pole trójkąta AFB na dwa sposoby, jako
![]() pola całego rombu i ze wzoru
pola całego rombu i ze wzoru
![]() . Przyrównaj do siebie te wzory, aby wyznaczyć zależność |BF| od a. Oblicz długość k z twierdzenia cosinusów dla trójkąta AFB.
. Przyrównaj do siebie te wzory, aby wyznaczyć zależność |BF| od a. Oblicz długość k z twierdzenia cosinusów dla trójkąta AFB.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
