W trójkącie równoramiennym do obu ramion poprowadzono środkowe. Oblicz: tangens kąta ostrego, który znajduje się między środkowymi w trójkącie prostokątnym.
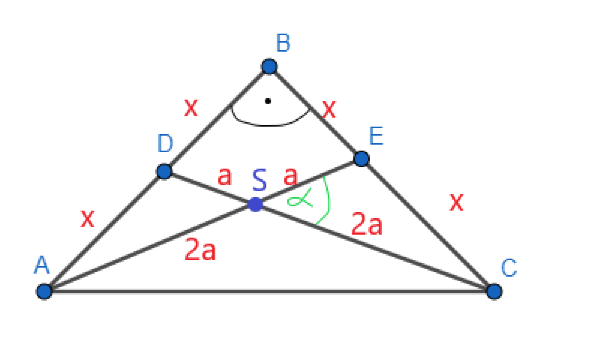
Z tw. Pitagorasa w DBC
![]()
![]()
![]()
![]()
Z tw. cosinusa w SEC
![]()
![]()
![]()
![]()
![]()
![]()
Z jedynki trygonometrycznej
![]()
![]()
![]()
![]() - ostry
- ostry
![]()
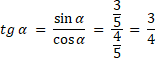

Przyjmij oznaczenia jak na rysunku. Środkowa dzieli bok na dwa równe odcinki, a miejsce przecięcia się środkowych dzieli je w stosunku 2 : 1 licząc od wierzchołka. Oblicz zależność x od a, korzystając z twierdzenia Pitagorasa w trójkącie DBC. Kolejno skorzystaj z twierdzenia cosinusów w trójkącie SEC, aby wyznaczyć miarę
![]() . Kolejno wyznacz
. Kolejno wyznacz
![]() z jedynki trygonometrycznej i oblicz
z jedynki trygonometrycznej i oblicz
![]() .
.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
