Oblicz pole trójkąta, którego wierzchołkami są punkty styczności okręgu wpisanego w trójkąt prostokątny o przyprostokątnych o długościach 6 i 8.
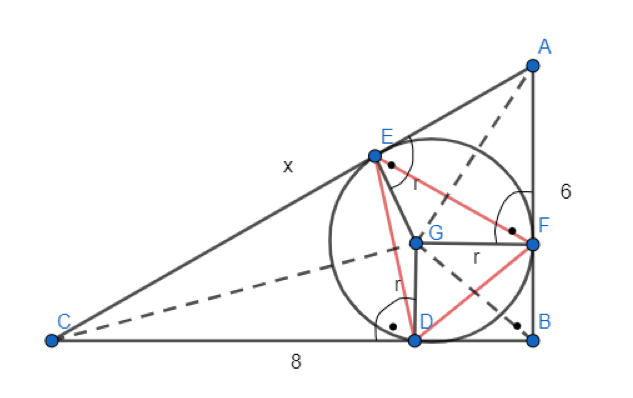
Z tw. Pitagorasa w ABC
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Trójkąt CED
![]()
|CD| = |CE| (z tw. o odcinkach stycznych)
![]()
![]()
Trójkąt EAF
|EA| = |AF| = |AB| - |FB| = 6 – 2 = 4
|EA| = |AF| (z tw. o odcinkach stycznych)
![]()
![]()
Trójkąt FBD
![]()
![]()

Zacznij od obliczenia długości x z twierdzenia Pitagorasa w trójkącie ABC. Kolejno oblicz pole tego trójkąta i skorzystaj ze wzoru
![]() , aby obliczyć długość r. Kolejno oblicz pola trójkątów CED, DBC i EAF i odejmij te pola od pola trójkąta ABC, aby obliczyć pole trójkąta EFD.
, aby obliczyć długość r. Kolejno oblicz pola trójkątów CED, DBC i EAF i odejmij te pola od pola trójkąta ABC, aby obliczyć pole trójkąta EFD.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
