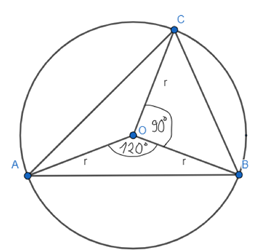
Trójkąt ABC został wpisany w okrąg o środku O. Oblicz miary kątów tego trójkąta, wiedząc, że kąt AOB wynosi 120° i kąt BOC wynosi 90°. Rozważymy wszystkie przypadki.
I przypadek
![]()
![]()
![]()
![]()
![]()
![]()
![]()
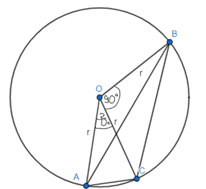
II przypadek
![]()
![]()
![]()
![]()
![]()
![]()

Rozważ dwa przypadki
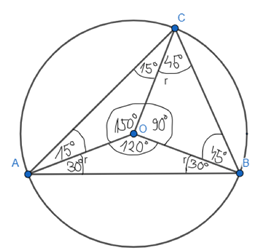
I przypadek – środek okręgu znajduje się w środku trójkąta
Zacznij od obliczenia miary kąta AOC. Następnie oblicz miary kątów przy podstawie w trójkątach AOC, COB i AOB, wiedząc, że wszystkie te trójkąty są równoramienne. Uzupełnij informacje na rysunku i oblicz miary kątów trójkąta ABC.
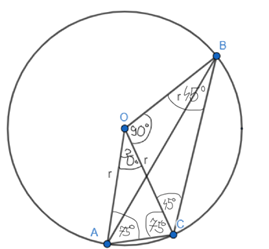
II przypadek – środek okręgu znajduje się poza środkiem trójkąta
Zacznij od obliczenia wartości kąta AOC. Następnie oblicz miary kątów przy podstawie w trójkątach AOC, COB i AOB, wiedząc, że wszystkie te trójkąty są równoramienne. Uzupełnij informacje na rysunku i oblicz miarę kąta przy wierzchołku C. Kąt AOC jest kątem środkowym, a kąt ABC jest kątem wpisanym i oba są opisane na tym samym łuku, więc kąt AOC jest dwa razy większy od kąta ABC. Oblicz miarę kąta BAC z sumy kątów w trójkącie ABC.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
