W okręgach
![]() w podanej kolejności leżą na prostej i są środkami okręgów o promieniach
w podanej kolejności leżą na prostej i są środkami okręgów o promieniach
![]() . Zadaniem jest ustalenie wzajemnego położenia każdych dwóch z tych trzech okręgów, jeżeli wiadomo, że
. Zadaniem jest ustalenie wzajemnego położenia każdych dwóch z tych trzech okręgów, jeżeli wiadomo, że
![]()
![]()
![]()
Okręgi
![]() są styczne zewnętrznie
są styczne zewnętrznie
![]()
![]()
![]()
3 < 15
![]()
![]() są rozłączne wewnętzrnie
są rozłączne wewnętzrnie
![]()
![]()
![]()
![]()
![]()
![]() przecinają się
przecinają się

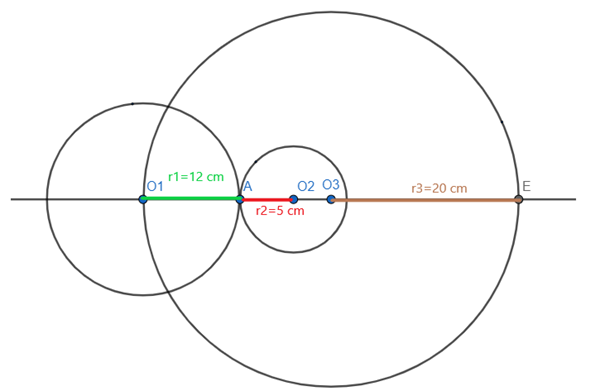
Zacznij od wykonania rysunku poglądowego.
Następnie skorzystaj z warunków:
Dwa okręgi są styczne zewnętrznie, jeśli suma ich promieni jest równa odległości między ich środkami.
Dwa okręgi są rozłączne wewnętrznie, jeśli różnica ich promieni jest większa od odległości między ich środkami.
Dwa okręgi przecinają się, jeśli odległość między ich środkami jest większa od różnicy ich promieni i mniejsza od sumy ich promieni.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
