Wyznacz pole powierzchni trójkąta o kątach
![]() , na którym został opisany okrąg, którego promień ma długość 4.
, na którym został opisany okrąg, którego promień ma długość 4.
![]()
![]()
![]()
![]()
![]()
Twierdzenie sinusów w △ABC
![]()
![]()
![]()
![]()
Z tw. cosinusów w AGB
![]()
![]()
![]()
W trójkącie ACD
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
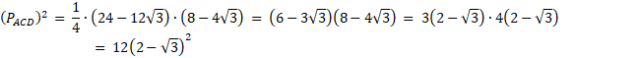
![]()
![]()
![]()

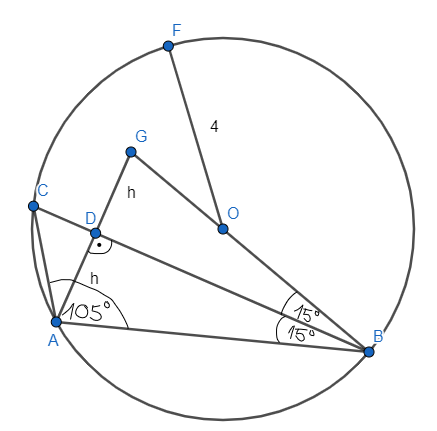
Wskazany trójkąt jest rozwartokątny, więc środek okręgu znajduje się poza nim. Oblicz miarę trzeciego kąta w tym trójkącie, a następnie poprowadź wysokość h opuszczoną na najdłuższy bok. Następnie zastosuj twierdzenie sinusów w trójkącie ABC, aby wyznaczyć długość AC. Następnie stwórz trójkąt DGB, będzie on symetryczny i przystający do trójkąta ABD, tak, że |AB| = |GB| =
![]() i |AD| = |DG| = h. Oblicz pole trójkąta AGB. Następnie oblicz pole trójkąta ADB, wiedząc, że to połowa pola trójkąta AGB. Wyznacz h z twierdzenia cosinusów w trójkącie AGB. Następnie korzystając z wartości
i |AD| = |DG| = h. Oblicz pole trójkąta AGB. Następnie oblicz pole trójkąta ADB, wiedząc, że to połowa pola trójkąta AGB. Wyznacz h z twierdzenia cosinusów w trójkącie AGB. Następnie korzystając z wartości
![]() , wyznacz długość |CD|. Możesz obliczyć tą długoś do potęgi drugiej i ostatecznie spierwiastkować w wyniku, dla wygody obliczeń. Oblicz pole trójkąta ACD i następnie pole trójkąta ABC.
, wyznacz długość |CD|. Możesz obliczyć tą długoś do potęgi drugiej i ostatecznie spierwiastkować w wyniku, dla wygody obliczeń. Oblicz pole trójkąta ACD i następnie pole trójkąta ABC.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
