Odległość środka okręgu wpisanego w trójkąt prostokątny od końców przeciwprostokątnej to
![]() . Oblicz długości boków tego trójkąta.
. Oblicz długości boków tego trójkąta.
![]()
![]()
![]()
![]()
![]()
![]()
Z tw. cosinusów w COB
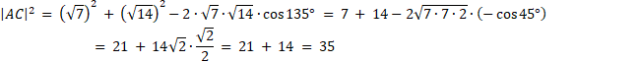
![]()
![]()
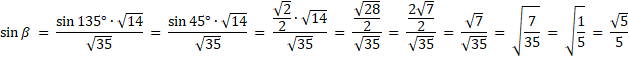
![]()
![]()
![]()
![]()
Z tw. Pitagorasa w AOE
![]()
![]()
![]()
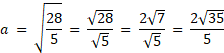
![]()
![]()
![]()
![]()

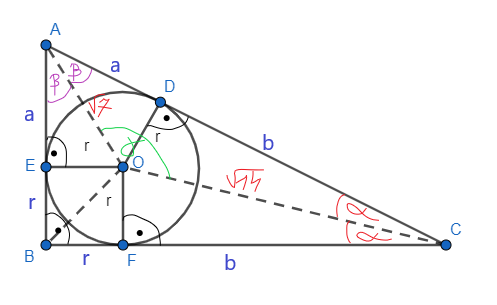
Skorzystaj z twierdzenia o odcinkach stycznych, aby stwierdzić, że |EA| = |AD|, |DC| = |CF|, |FB| = |BE|. Oblicz miarę
![]() , wiedząc, że ABC to trójkąt prostokątny. Następnie oblicz miarę kąta
, wiedząc, że ABC to trójkąt prostokątny. Następnie oblicz miarę kąta
![]() . Kolejno wyznacz miarę boku |AC| z twierdzenia cosinusów w trójkącie COA. Kolejno wyznacz miarę kąta
. Kolejno wyznacz miarę boku |AC| z twierdzenia cosinusów w trójkącie COA. Kolejno wyznacz miarę kąta
![]() z twierdzenia sinusów w trójkącie COA. Znając wartość
z twierdzenia sinusów w trójkącie COA. Znając wartość
![]() , oblicz r. Kolejno z twierdzenia Pitagorasa w trójkącie AOE oblicz a. Znając wartość a, oblicz wartość b i wypisz długości boków trójkąta.
, oblicz r. Kolejno z twierdzenia Pitagorasa w trójkącie AOE oblicz a. Znając wartość a, oblicz wartość b i wypisz długości boków trójkąta.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
