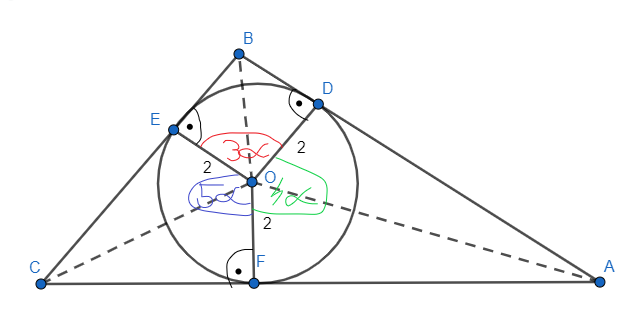
Oblicz pole trójkąta, w który został wpisany okrąg o promieniu 2, przy założeniu, że punkty styczności okręgu z bokami trójkąta podzieliły go na trzy łuki, których stosunek długości wynosi 3:4:5.
![]()
![]()
![]()
![]()
![]()
|EO| = |OD| = |DB| = |BE| = 2
![]()
![]()
![]()
![]()
![]()
|FA| = |AD| =
![]()
|EC| = |CF| = x
Z tw. Pitagorasa w trójkącie CBA
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
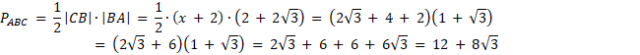

Punkty styczności okręgu z bokami trójkąta podzieliły go na trzy łuki, których stosunek długości wynosi 3:4:5, stosunek kątów środkowych, które powstały przez podział również wynosi 3 : 4 : 5. Oblicz miarę kąta
![]() , a następnie miary kątów FOD, DOE i EOF. Zauważ, że czworokąt EODB jest kwadratem, wiec |EO| = |OD| = |DB| = |BE| = 2. Zauważ, że długość OA jest dwusieczną kąta COD, czyli kąty FOA i AOD są równe i oba mają po
, a następnie miary kątów FOD, DOE i EOF. Zauważ, że czworokąt EODB jest kwadratem, wiec |EO| = |OD| = |DB| = |BE| = 2. Zauważ, że długość OA jest dwusieczną kąta COD, czyli kąty FOA i AOD są równe i oba mają po
![]() . Skorzystaj z
. Skorzystaj z
![]() w trójkącie FAO, aby obliczyć długość |FA|. Skorzystaj z twierdzenia o odcinkach stycznych, aby stwierdzić, że |FA| = |AD|, |EC| = |CF|. Oznacz długości odcinków EC i CF jako x. Oblicz wartość x korzystając z twierdzenia Pitagorasa w trójkącie CBA. Na koniec oblicz pole trójkąta ABC.
w trójkącie FAO, aby obliczyć długość |FA|. Skorzystaj z twierdzenia o odcinkach stycznych, aby stwierdzić, że |FA| = |AD|, |EC| = |CF|. Oznacz długości odcinków EC i CF jako x. Oblicz wartość x korzystając z twierdzenia Pitagorasa w trójkącie CBA. Na koniec oblicz pole trójkąta ABC.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
